2 Расчет сборного многопролетного ригеля

2.1 Определение расчетных пролетов ригеля

Расчетный пролет ригеля (рис.1.7) в крайних пролетах принимается

равным расстоянию от оси его опоры на стене до оси колонны:

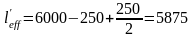мм

Расчетный пролет ригеля в средних пролетах принимается равным

расстоянию между осями leff=6000мм.

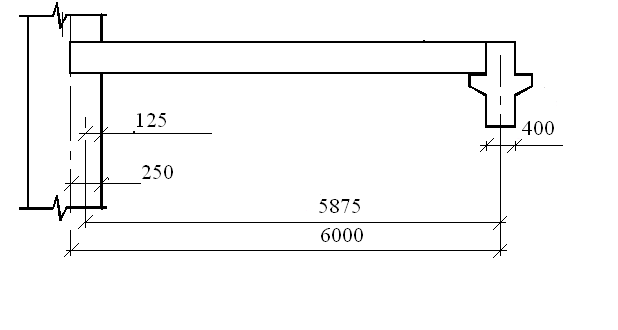
Рисунок 2.1 – Расчётный пролёт ригеля

2.2. Определение нагрузки на ригель

Зададимся поперечным сечением ригеля исходя из следующих

соотношений:

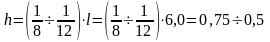(м);

Принимаем h=0,6 м.

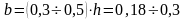м;

Принимаем b=0,25.

Таблица 2.1 - Нагрузки на 1 м² сборного перекрытия

Вид нагрузки	Нормативная нагрузка, кН/м2	Коэффициент безопасности по нагрузке [1, таблица 5]	Расчетная нагрузка, кН/м2
Постоянная от слоя цементно-песчаного раствора (δ=0,02 м, ρ=18 кН/м3)	0,36	1,35	0,486
от керамической плитки (δ=0,01 м, ρ=24 кН/м3)	0,24	1,35	0,324
от собственного веса	2,83	1,35	3,821
Итого	gk=3,43		gd= 4,631
Переменная полезная (по зданию)	qk=5,4	1,5	qd= 8,1
Всего	(g+q)k =8,83		(g+q)d=12,731

Расчетные нагрузки на 1 погонный м ригеля при ширине грузовой площади

7,8 м и коэффициента надежности по назначению здания γn= 0,95 составят:

Постоянная g_d =4,631∙7,8∙0,95=34,316 кН/м.

суммарная (с учётом нагрузки от ригеля) постоянная:

g_d =34,316+(0,25∙0,6∙25∙1,35∙0,95)=39,125 кН/м.

переменная q_d=8,1∙7,8∙0,95= 60,02 кН/м.

Суммарная нагрузка будет равна (g+q)_d = 39,125+60,02=81,139 кН/м.

Первое основное сочетание:

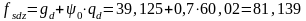кН/м,

Второе основное сочетание:

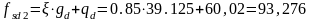кН/м.

Для дальнейших расчетов принимаем второе сочетание как наиболее не благоприятное.

2.3 Построение эпюр изгибающих моментов

Определение изгибающих моментов и поперечных сил ригеля производится с учетом перераспределения усилий в стадии предельного состояния конструкции. Первоначально необходимо рассчитать ригель как упругую систему на действие постоянных нагрузок и отдельных схем невыгодного расположения временных нагрузок. Для расчёта по таблицам многоэтажную раму делим на одноэтажные трёхпролётные рамы, рассматриваемые как балки на упруговращающихся опорах. Моменты в крайних пролётах принимаем по моменту в первом пролёте, моменты во всех средних пролётах принимают равными моментам среднего пролёта трёхпролётной рамы.

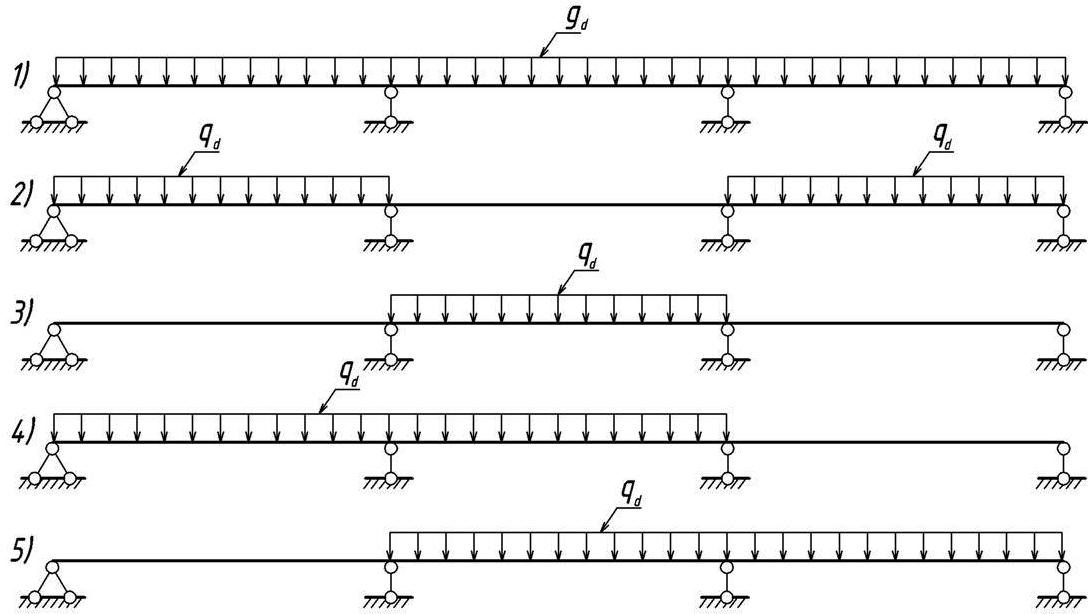
Рисунок 2.2 – Варианты нагружения

Рассмотрим следующие варианты загружения (табл. 2.2):

Таблица 2.2 – Варианты загружения

Варианты загружения	Сочетание нагрузок
1	1+2
2	1+3
3	1+4
4	1+5

Опорные моменты вычисляют по таблице 1П14[1] для ригелей, соединенных с колоннами на средних и крайних опорах шарнирно, по формуле:

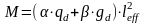
где

α и β – табличные коэффициенты зависящие от схем загружения ригеля и коэффициента κ – отношения погонных жёсткостей ригеля и колонны.

Вычисляем:

,

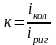где

i – погонная жёсткость ригеля и колоны, ;

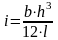Геометрические характеристики колонны: b=h=0,4 м, l=3,6 м,

где

l – высота этажа,

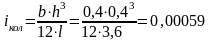м³;

Геометрические характеристика ригеля: b=0,25 м, h=0,6 м, l= 6,0 м.

i м³.

.

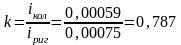По таблице 1[5] в зависимости от значения к определяем опорные моменты.

Если найденного значения κ нет в таблице, то следует провести интерполяцию, либо экстраполяцию.

Вариант 1

Таблица 2.3 – Постоянная нагрузка, действующая на плиту

Схема нагружения		Опорные моменты
		М21	М23	М43
α	1	-0,1187	-0,0886	-0,0886
β	2	-0,105	-0,0137	-0,0137

Определим опорные моменты:

кН·м

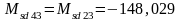кН·м

кН·м.

Моменты в пролетах определяем по формуле:

.

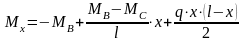Максимальные изгибающие моменты в пролетах возникают на расстоянии .

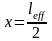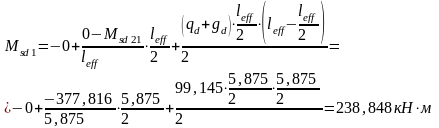
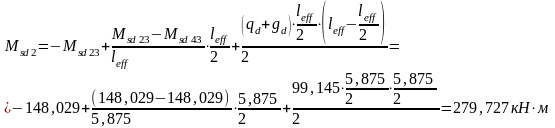
Т.к. нагрузка на первом варианте загружения приложена симметрично, то

М_sd3=M_sd1=238,848 кН·м, М_sd45 =М_sd21= - 377,816 кН·м.

Вариант 2

Таблица 2.4 – Постоянная нагрузка, действующая на плиту

Схема нагружения		Опорные моменты
		М21	М23	М43
α	1	-0,1187	-0,0886	-0,0886
β	3	-0,012	-0,0757	-0,0757

Определим опорные моменты:

кН·м

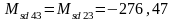кН·м

кН·м.

Моменты в пролетах определяем по формуле:

.

Максимальные изгибающие моменты в пролетах возникают на расстоянии .

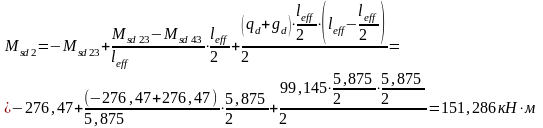
М_sd3=M_sd1=335,179 кН·м, М_sd45 =М_sd21= - 185,155 кН·м

Вариант 3

Таблица 2.5 – Постоянная нагрузка, действующая на плиту

Схема нагружения		Опорные моменты
		М21		М23		М43
α	1		-0,1187		-0,0886		-0,0886
β	4		-0,1209		-0,0974		-0,0671

Определим опорные моменты:

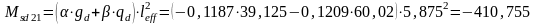кН·м

кН·м

.

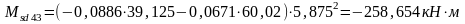Моменты в пролетах определяем по формуле:

.

Максимальные изгибающие моменты в пролетах возникают на расстоянии .

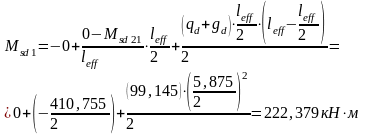
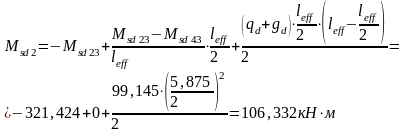
Вариант 4.

Таблица 2.6 – Постоянная нагрузка, действующая на плиту

Схема нагружения		Опорные моменты
		М21		М23		М43
α	1		-0,1187		-0,0886		-0,0886
β	4		-0,1209		-0,0974		-0,0671

Определим опорные моменты:

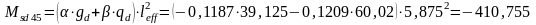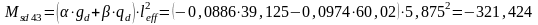кН·м

кН·м

.

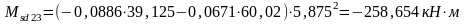Моменты в пролетах определяем по формуле:

.

Максимальные изгибающие моменты в пролетах возникают на расстоянии .

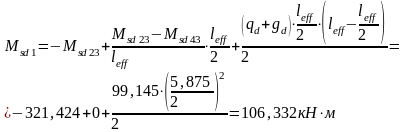
Таблица 2.6 – Изгибающие моменты в ригеле

Вариант нагружения	Сечения
	1	2 слева	2 справа	3	4 слева	4 справа	5
1	238,848	-377,816	-148,029	279,727	-148,029	-377,816	238,848
2	335,179	-185,155	-276,47	151,286	-276,47	-185,155	335,179
3	222,379	-410,755	-321,424	106,332	-258,654	-	-
4	-	-	-258,654	106,332	-321,424	-410,755	222,379
Мmax	335,179	-410,755	-321,424	279,727	-321,424	-410,755	335,179

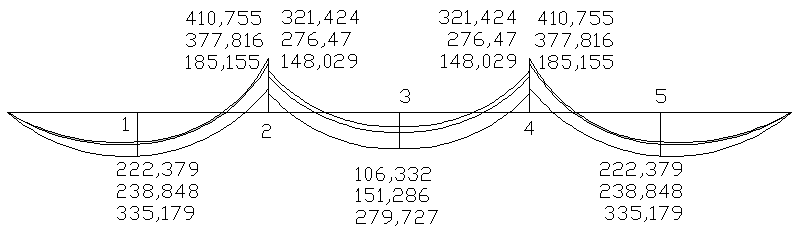
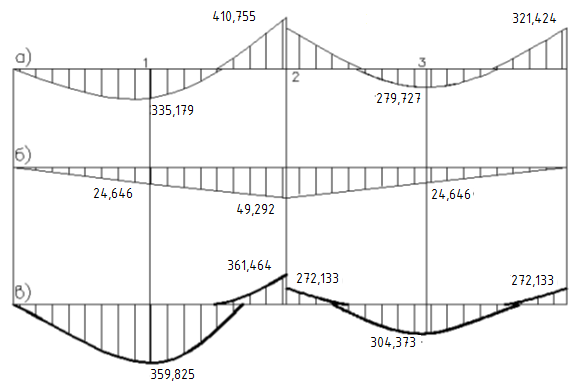
Рисунок 2.3- Эпюра изгибающих моментов с учётом возникновении пластического шарнира