8. Геостатистическое оценивание

Основной геостатистической моделью, которая в том или ином виде ис­пользуется во всех методах геостатистики, является кригинг (kriging) — линейный интерполятор, использующий для получения оценки значения функции в некоторой точке пространства x₀ экспериментально измеренные значения этой функции в других точках:

(2.11)

Для определения весов w_i(x₀) могут быть использованы различные детер­министические методы, например веса могут браться обратно пропорцио­нальными расстоянию от измеренной точки до оцениваемой или в соответ­ствии с каким-либо другим предположением о природе связей в данных. Однако все эти методы пренебрегают использованием информации о струк­туре внутренней корреляции пространственных данных.

Следующим критерием при построении модели является условие несмещен­ности оценки, что эквивалентно условию

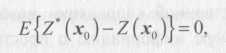(2.12)

где Z(x₀) — истинное (неизвестное) значение оцениваемой функции в точ­ке x₀. Иными словами, ошибки интерполяции должны иметь в каждой точке среднее, равное нулю. Это условие может быть реализовано и в рамках де­терминистических подходов.

Еще одно условие, которое мы хотим наложить, — оптимальность интерпо­ляции в смысле минимизации вариации ошибки оценки, т. е. веса w_i линей­ной регрессии в уравнении (2.11) должны быть выбраны так, чтобы мини­мизировать значение вариации ошибки оценки:

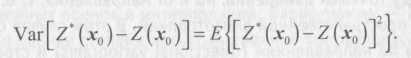(2.13)

Таким образом, кригинг является наилучшим (в смысле минимума вариации оценки) линейным и несмещенным оценивателем (the best Linear unbiased estimator — BLUE). В процессе поиска минимума вариации (2.13) ключе­вую роль играет использование модели вариограммы исходных данных. В результате поиска весовых коэффициентов для получения оценки, удо­влетворяющей всем перечисленным условиям, удается оценить и значение вариации (2.13), которое может интерпретироваться как описание точности кригинговой оценки.

9. Проверка качества модели - кросс-валидация

При использовании той или иной модели интерполяции крайне важно пра­вильно подобрать значения модельно-зависимых параметров. Для кригинга такими параметрами являются параметры модели вариограммы. При работе с реальными данными не всегда удается сразу выбрать теоретическую мо­дель экспериментальной вариограммы. Для проверки качества выбранной модели используют различные количественные методы: кросс-валидацию (cross-validation), метод складного ножа (jack-knife), бутстреп (bootstrap).

Кросс-валидация наиболее простой и часто использующийся не только в геостатистике подход при сравнении результатов, получаемых различными методами или одним и тем же методом, но с различными параметрами. Вы­полняется кросс-валидация следующим образом:

• из базы данных временно изымается одна точка, и для нее проводится оценка значения;

• полученное значение сравнивается с известным, и вычисляется невяз­ка разница между измеренными и оцененными значениями:

первые два шага проводятся для всех точек базы данных.

Полученные невязки ΔZ(x) могут быть графически представлены в виде карты (карты невязок), по которой можно посмотреть, в каких зонах метод срабатывает лучше, а в каких хуже. Вместо невязок можно визуализировать относительные ошибки:

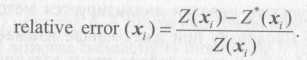
Полезно также представить результаты кросс-валидации в виде графика Y(Z(x))=Z^*(х) или аналогичного ему — Y(Z(x)) = Δ(x). Проведение на таком графике биссектрисы (или соответственно прямой Y = 0), соот­ветствующей равенству оценки и исходного значения, позволяет видеть характер отклонения: большее отклонение для высоких или для низких значений Z, какие-либо тренды в поведении оценки и т. п. Вместе с тем, на графиках невязок можно проследить эффект сглаживания — область низких значений в среднем переоценивается, а область высоких значении недооценивается.

Кроме локальных характеристик кросс-валидация позволяет оценить и гло­бальные характеристики оценки для сравнения:

1. Смещение Δm = т - т*, где т — среднее, оцененное по исходным дан­ным; т* — среднее, оцененное по полученным результатам.

2. Сумму квадратов невязок:

где R - штрафной член, вводящийся для контроля количества неоце­ненных точек.

3. Среднюю квадратичную ошибку (root mean square error RMSE):

4. Коэффициент эффективности:

5. Коэффициент корреляции ρ, угол наклона регрессионной прямой на графике Y(Z(x)) = Z^*(х).

Вообще говоря, кросс-валидация — это частный случай метода складного ножа, когда выбираемый набор состоит из одной точки (leave-one-out).

Метод складного ножа (jack-knife) является общим случаем кросс-валидации, когда оценивание проводится не в одной, а в нескольких точках из­мерений, данные о которых предварительно изымаются из рассмотрения. Полученные в результате невязки анализируется методом, аналогичным описанному выше. Поскольку при джек-найфе изымается произвольный набор данных, комбинации этого набора могут варьироваться, что делает этот метод стохастическим.

Бутстреп (bootstrap) состоит в оценке на основе случайных выборок из набора данных. Выборки делаются из исходного набора случайным обра­зом. Выбранная точка не изымается, она может попасть в выборку несколь­ко раз. Оценка проводится по оставшимся не выбранными точкам. Обычно процедура выборки и оценки повторяется много раз.

Литература

Cressie N. Statistics for spatial data. — New York: John Wiley & Sons,

1991. —900 p.

Deutsch C. DECLUS: a FORTRAN 77 program for determining optimal declustering weights // Computers and Geosciences. — 1989. —Vol. 15. — P. 325—332.

Deutsch С. V, Journel A. G. GSLIB: Geostatistical Software Library and User’s Guide. —-New York; Oxford: Oxford Univ. Press, 1998. — 369 p. Engineering and Design: Practical aspects of applying geostatistics at hazardous, toxic and radioactive waste sites: Technical Letter ETL 1110-1-175 / Department of the US Army. — Washington, 30 June 1997. — 93 p.

Goovaerts P. Geostatistics for Natural Resources Evaluation. — [S. 1.]:

Oxford Univ. Press, 1997.

Hengl T. Finding the right pixel size // Computers and Geosciences. —

2006. — Vol. 32. — P. 1283—1298.

Isaaks E. H., Srivastava R. M. An Introduction to Applied Geostatistics. — Oxford: Oxford Univ. Press, 1989.

Journel A. G. Nonparametric estimation of spatial distributions // Mathematical Geology. — 1983. — Vol. 15. — P. 445—468.

Journel A. G._y Huijbregts Ch. J. Mining Geostatistics. — London: Academic Press, 1978. — 600 p.

Mandelbrot В. В. The fractal theory of nature. —New York: Freeman, 1982. Morishita M. Measuring of the dispersion and analysis of distribution patterns // Memoires of the Faculty of Science, Kyushu University. Series E. Biology. — 1959. — Vol. 2. — P. 215—235.

Preparata F. P, Shamos М. I. Computational Geometry. — New York: Springer-Veri., 1985. —P. 198—218.

Библиография по геостатистике

1. Cressie N. Statistics for spatial data. — New York: John Wiley & Sons,

2. 1991. —900 p.

3. Deutsch C. DECLUS: a FORTRAN 77 program for determining optimal declustering weights // Computers and Geosciences. — 1989. —Vol. 15. — P. 325—332.

4. Deutsch С. V, Journel A. G. GSLIB: Geostatistical Software Library and User’s Guide. —-New York; Oxford: Oxford Univ. Press, 1998. — 369 p. Engineering and Design: Practical aspects of applying geostatistics at hazardous, toxic and radioactive waste sites: Technical Letter ETL 1110-1-175 / Department of the US Army. — Washington, 30 June 1997. — 93 p.

5. Goovaerts P. Geostatistics for Natural Resources Evaluation. — [S. 1.]:

6. Oxford Univ. Press, 1997.

7. Hengl T. Finding the right pixel size // Computers and Geosciences. —

8. 2006. — Vol. 32. — P. 1283—1298.

9. Isaaks E. H., Srivastava R. M. An Introduction to Applied Geostatistics. — Oxford: Oxford Univ. Press, 1989.

10. Journel A. G. Nonparametric estimation of spatial distributions // Mathematical Geology. — 1983. — Vol. 15. — P. 445—468.

11. Journel A. G._y Huijbregts Ch. J. Mining Geostatistics. — London: Academic Press, 1978. — 600 p.

12. Mandelbrot В. В. The fractal theory of nature. —New York: Freeman, 1982. Morishita M. Measuring of the dispersion and analysis of distribution patterns // Memoires of the Faculty of Science, Kyushu University. Series E. Biology. — 1959. — Vol. 2. — P. 215—235.

13. Preparata F. P, Shamos М. I. Computational Geometry. — New York: Springer-Veri., 1985. —P. 198—218.

14. Raes F., Graziani G., Girardi F. A simple and fractal analysis of the European on-line network for airborne radioactivity monitoring // Environmental Monitoring and Assessment. — 1991. —Vol. 18. — P. 221—234.