5. Декластеризация

Большая часть пространственно распределенных данных, которые анали­зируются в геостатистике, имеет кластерную структуру. Кластер образу­ется, если в одной области было проведено значительно большее число измерений, чем в другой. В этом случае могут возникнуть существенные искажения при вычислении, например среднего значения. Это влечет не­возможность получить репрезентативную гистограмму распределения. Пусть, например, в области высоких значений измеряемой величины, нахо­дится вдвое больше точек, чем в области низких значений. Если при оцен­ке среднего и других статистических параметров все значения будут иметь одинаковый вес, то область высоких значений будет слишком сильно вли­ять на такую оценку. В этом случае точки из зоны с большими значениями нужно было бы учитывать с весом, вдвое меньшим, чем все остальные. Проблема вычисления статистического веса каждой точки в параметрах распределения решается путем проведения процедуры декластеризации (declustering) данных.

Декластеризация не требуется, если измерения были выполнены на регу­лярной сетке. В этом случае наилучшее описание распределения получится при работе с равными весами. Тем не мене, во многих случаях невозможно получить данные на равномерной сетке.

При анализе измерений, проведенных на нерегулярной сетке, предполага­ется существование такого набора весов, при котором может быть получе­но репрезентативное распределение данных. Здравый смысл подсказыва­ет, что данные из области с большей плотностью измерений нужно брать с меньшим весом (для уменьшения их влияния на распределение в целом), чем данные из области с меньшей плотностью измерений. Для вычисления весов могут быть использованы разные подходы: метод ячейковой декла­стеризации, метод ячеек Дирихле (полигонов Вороного, рис. 4), кригинг.

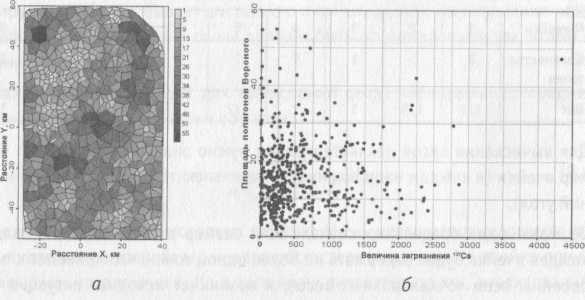
Рис. 4. Площади полигонов Вороного (а), корреляция площади полигона и величины пространственной переменной 137Cs (6)

Метод ячейковой декластеризации (cell-dedustering) был предложен в [Journel 1983]. Его идея заключается в разбиении рассматриваемой области на подобласти кластеризованных данных и в определении равных весов для всех точек внутри каждой подобласти в соответствии с их количеством.

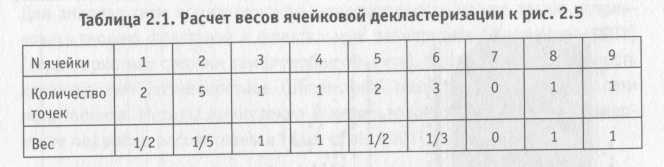
Так, если в ячейку а_к попало п_к точек, то каждое измерение будет учтено с ве­сом 1/п_к. Область а_к пространства обычно имеет размерность 3 (время может стать четвертым измерением). Для ячейки, не содержащей опытных точек, веса не рассчитываются, т. е. область декластеризованных данных состоит из ячеек, содержащих по крайней мере по одному измерению. Это ограничи­вает влияние граничных данных весом 1,0. На рис. 5 показан пример раз­биения области на ячейки. Расчет соответствующих весовых коэффициентов приведен в табл. 1. После вычисления весов в такой форме они должны быть отнормированы так, чтобы их сумма была равна 1.

Рис. 5. Пример расчета весов ячейковой декластеризации

Таб. 1. Расчёт весов ячейковой декластеризации к рис. 5

Для вычисления весов декластеризации нужно знать два параметра: раз­мер ячейки (в каждом направлении) и начальную точку сетки (левый ниж­ний угол).

Возможны два предельных случая: если размер ячейки слишком мал, то каждая ячейка будет содержать не более одной точки, что приведет к при­своению всем точкам равных весов, и возникнет исходная ситуация недекластеризованных данных. В противоположном случае, когда размер ячейки слишком велик, все данные попадут в одну единственную ячейку и результат будет тот же — все точки получат равные веса.

Метод выбора размера ячейки зависит от типа кластеризации. Если данные кластеризованы случайным образом (есть области скопления точек, никак не связанных с их значениями), размер ячейки выбирается так, чтобы в об­ластях с низкой плотностью измерений на одну ячейку приходилось при­близительно по одной точке измерений. Если же известно, что есть области высоких или низких значений с большим количеством измерений, то раз­мер ячейки может быть выбран так, чтобы оптимально получить максималь­ное или минимальное взвешенное среднее. При декластеризации областей высоких или низких значений нужно пробовать наборы ячеек разного раз­мера. В этом случае строится график зависимости взвешенного среднего значения от размера ячейки (Рис. 7) и в соответствии с ним выбирается подходя­щий размер [Deutsch, 1989].

Ячейки не обязательно должны быть квадратными. С помощью параметра анизотропии (отношение размеров ячейки) можно построить описанные выше зависимости и на их основе также выбрать параметры ячейки, соот­ветствующие минимуму или максимуму взвешенного среднего. Результаты можно представить, например, в виде контурной карты с размерами ячеек в каждом из направлений в качестве координат.

Если при фиксированном размере ячейки перемещать начало декластери­зующей сетки, то веса декластеризации могут существенно меняться. Чтобы исключить влияние этого фактора, проводят несколько шагов декластери­зации, вводя систематическое смещение начала сетки. Веса, полученные после каждого шага смещения, нормируются на единицу, и результаты сум­мируются. Обычно бывает достаточно пяти смещений. По окончании мани­пуляций веса всех точек снова должны быть отнормированы так, чтобы их сумма была равна 1.

Таким образом, формулу для вычисления декластеризованного среднего можно записать следующим образом:

(2.6.)

где,

п — общее число исходных данных; N_of — число использующихся при вычислении смещений; w_ik — веса декластеризации для к-й ячейки при i-м смещении начала ячеек. Но в алгоритме декластеризации, реализованном в популярном пакете геостатистических программ GSLib [Deutsch, Journel, 1998], используется нормализация весов не к 1, а к числу измерений. При этом формула для вычисления декластеризованного среднего (2.6) не­сколько изменяется:

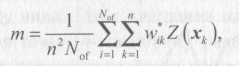(2.7)

где w_ik — веса декластеризации, связанные с весами из (2.6) соотношени­ем w_ik=nw_ik.

На рис. 6 приведены значения весов ячейковой декластеризации по фор­муле (2.7) для данных по радиоактивному загрязнению изотопом 137Cs по­чвы. На рис. 7 для тех же данных приведен график зависимости декластеризованного среднего от размера декластеризующей ячейки. Что­бы компенсировать влияние кластеров высоких значений, следует, видимо, выбрать ячейку размером 75 км.

Рис. 6. Веса ячейковой декластеризации для декластеризации кластеров низких значений (а) и кластеров высоких значений (б)

Рис. 7. Зависимость декластеризованного среднего значения от размера ячейки.

Метод ячейковой декластеризации.

Рис. 8. Гистограммы декластеризованных и исходных данных ¹³⁷Cs