4. Сеть мониторинга и кластерность

Простейшим общепринятым видом визуализации данных является нанесе­ние точек на плоскость пространственных координат, причем цвет нанесен­ной точки может соответствовать измеренной в них величине (рис. 1а).

Рис. 1. Диаграмма расположения точек измерений (а), триангуляция сети монито­ринга (б), полигоны Вороного (в) и контуры данных измерений по триангуляции (г)

Для визуализации сети мониторинга и ее кластерной структуры часто ис­пользуется триангуляция Делоне [Preparata, Shamos, 1985] — система тре­угольников с вершинами в точках измерений, непересекающимися ребрами и минимальным количеством тупоугольных треугольников (рис. 2.16). Та­кая визуализация позволяет качественно обособить области с повышенной плотностью измерений — с кластерами. Кроме того, триангуляция Делоне строит систему соседства: точки, которые соединены друг с другом ребра­ми треугольников, являются ближайшими соседями по отношению друг к другу.

Триангуляция также является основой для построения простейшего мето­да линейной интерполяции: три точки в пространстве (вершины треуголь­ников) однозначно определяют плоскость, в пределах которой значения функции вычисляются согласно геометрическим принципам (рис. 2.1г). Другим видом визуализации данных являются полигоны Вороного, или, как их еще называют, разбиение Тиссена, ячейки Дирихле и области влияния. Полигон Вороного P_f построенный для точки измерений x_f характеризу­ется тем, что содержит те и только те точки, расстояние от которых до точ­ки х меньше или равно расстоянию до любой другой точки измерений х. (рис. 2.1в). При построении полигонов Вороного используется система со­седства, полученная в процессе триангуляции Делоне. Границы полигона Вороного Р. состоят из отрезков серединных перпендикуляров, проведен­ных к сторонам треугольников Делоне. Полигоны Вороного можно исполь­зовать как разрывную интерполяционную оценку (оценка по ближайшему соседу). Для этого каждой точке, попавшей в полигон, присваивается зна­чение, соответствующее его материнской точке. Эти полигоны также ис­пользуются в задачах пространственной классификации — классификация по ближайшему соседу.

Для визуализации сети мониторинга и ее кластерной структуры часто ис­пользуется триангуляция Делоне [Preparata, Shamos, 1985] — система тре­угольников с вершинами в точках измерений, непересекающимися ребрами и минимальным количеством тупоугольных треугольников (рис. 1б). Та­кая визуализация позволяет качественно обособить области с повышенной плотностью измерений — с кластерами. Кроме того, триангуляция Делоне строит систему соседства: точки, которые соединены друг с другом ребра­ми треугольников, являются ближайшими соседями по отношению друг к другу.

Триангуляция также является основой для построения простейшего мето­да линейной интерполяции: три точки в пространстве (вершины треуголь­ников) однозначно определяют плоскость, в пределах которой значения функции вычисляются согласно геометрическим принципам (рис. 1г).

Другим видом визуализации данных являются полигоны Вороного, или, как их еще называют, разбиение Тиссена, ячейки Дирихле и области влияния. Полигон Вороного P_f построенный для точки измерений x_f характеризу­ется тем, что содержит те и только те точки, расстояние от которых до точ­ки х меньше или равно расстоянию до любой другой точки измерений х. (рис. 1в). При построении полигонов Вороного используется система со­седства, полученная в процессе триангуляции Делоне. Границы полигона Вороного P_f состоят из отрезков серединных перпендикуляров, проведен­ных к сторонам треугольников Делоне. Полигоны Вороного можно исполь­зовать как разрывную интерполяционную оценку (оценка по ближайшему соседу). Для этого каждой точке, попавшей в полигон, присваивается зна­чение, соответствующее его материнской точке. Эти полигоны также ис­пользуются в задачах пространственной классификации — классификация по ближайшему соседу.

Для выявления особенностей, а именно наличия кластерных структур или разреженностей в сети мониторинга (наборе точек измерений), проводят анализ сети мониторинга. Простейшими методами такого анализа мож­но считать описание топологии сети с помощью гистограммы расстояний между точками (рис. 2а) и гистограммы площадей полигонов Вороного (рис. 2б). Гистограмма в данном случае — это график числа каких-либо событий (числа пар точек или числа полигонов), попавших в какой-либо интер­вал значений.

Рис.2. Гистограмма расстояний между точками (а) и гистограмма площадей по­лигонов

Вороного (б)

При равномерном распределении точек в пространстве число пар должно быть одинаково для всех расстояний (или уменьшаться при увеличении расстояния за счет граничного эффекта). Рост числа пар с ростом рас­стояния между точками свидетельствует о наличии кластеров. Гистограм­ма площадей полигонов для регулярной сетки должна представлять собой дельта-функцию (один пик), так как все полигоны одного размера. Любые искажения (широкий пик, длинный хвост, несколько пиков) означают при­сутствие каких-либо особенностей в сети.

Другим методом анализа сети мониторинга является статистический подход [Cressie, 1991], рассматривающий точки измерений как случайный точечный процесс. Характеризовать распределение точек можно с использованием статистических индексов. Примером такого подхода является диаграмма Моришита. Индекс Моришита вычисляется для области, разбитой на пря­моугольные ячейки равного размера, по формуле [Morishita, 1959]

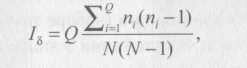
где,

N — полное число точек сети мониторинга;

Q — число ячеек разбиения;

п_i (i = 1, 2,...,Q) — число точек сети мониторинга, попавших в ячейку. Этот индекс характеризует вероятность того, что при выборе двух случай­ных точек они окажутся в одной ячейке.

Диаграмма Моришита представляет собой зависимость индекса Моришита от размера ячейки разбиения. Суще­ствуют три типа характерного поведения диаграммы Моришита, комбинации которых позволяют судить о характеристиках сети мониторинга:

• величина индекса Моришита с ростом размера ячейки растет и стремится к 1; тогда распределение точек можно считать равномерным;

• величина индекса Моришита не зависит от размера ячейки и примерно равна 1 (колеблется около 1); это означает, что распределение точек случайно и не имеет кластерных структур.

• величина индекса Моришита с ростом размера ячейки уменьшается или растет выше 1 — распределение точек сети кластерное.

• величина индекса Моришита с ростом размера ячейки растет и стремится к 1; тогда распределение точек можно считать равномерным;

• величина индекса Моришита не зависит от размера ячейки и примерно равна « 1 (колеблется около 1); это означает, что распределение точек случайно и не имеет кластерных структур.

• величина индекса Моришита с ростом размера ячейки уменьшается или растет выше 1 — распределение точек сети кластерное.

На рис. 3 приведены примеры диаграмм Моришита для различных типов се­тей мониторинга. Так, в случае мониторинга на регулярной равномерной сетке диаграмма имеет вид гладкой кривой логарифмического типа, стремящейся к единице (рис. 3а). При наличии многочисленных кластеров в плотной сети мониторинга кривая Моришита изобилует точками перегиба, которые харак­теризуют размеры различных кластеров (рис. 3б). В случае произвольного мониторинга с несколькими четко выраженными кластерами кривая Моришита имеет более гладкий вид и уменьшается, стремясь к единице (рис. 3в). Раз­мер кластеров характеризуют в этом случае точки изменения кривизны.

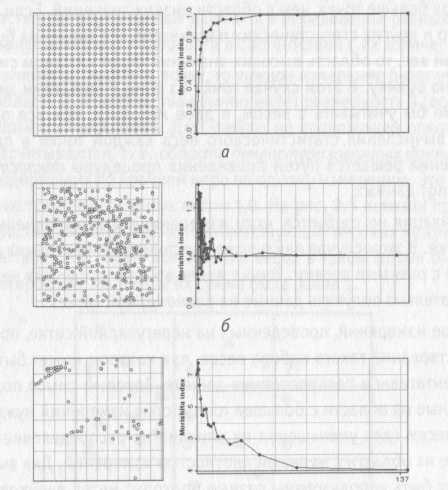
Рис. 3. Примеры диаграммы Моришита для различных сетей мониторинга: регу­лярная равномерная сеть (а), произвольная сеть со слабой кластерной структурой (б), произвольная слабо связанная кластеризованная сеть (в)