Лекция 1 Задачи анализа пространственных данных

Вопросы для обсуждения:

1. Проблемы пространственного моделирования

2. Постановка задачи

3. Подходы к анализу пространственно распределенных данных

4. Основные этапы анализа и моделирования пространственных данных

1. Проблемы пространственного моделирования

Существует огромное количество пространственно распределенной инфор­мации, собранной в базы и банки данных по окружающей среде. Задача ее интерпретации, анализа и дальнейшего использования представляется чрез­вычайно важной и требует комплексного системного подхода. Статистическое моделирование пространственных явлений позволяет обобщить имеющиеся измерения и получить модель их распределения в пространстве.

Анализ и моделирование про­странственных данных с использованием статистических методов позволяет ответить на ряд вопросов:

1). Как построить карту загрязнения?

2). Можно ли обойтись простыми методами интерполяции?

3). Можно ли дать однозначный ответ о том, где проходит граница повышенного уровня загрязнения?

Наиболее распространенной проблемой при работе с пространственно рас­пределенными данными является получение пространственной оценки. При этом, также важен вопрос о качестве и точности получаемых карт, неопре­деленности оценки, чувствительности использованных методов интерполя­ции и т.п.

Пространственное моделирование применяется во многих сферах челове­ческой деятельности. Так, при климатическом моделировании анализиру­ются измерения температуры, осадков, скорости ветра и т. д. в различных точках пространства. При моделировании загрязнения окружающей среды используются измерения (пробы грунта, воды, воздуха, дистанционное зондирование) в различных местах. В задачах геологии моделируются свойства пород в промежутке между скважинами, где делаются измерения. В медицинской географии анализируются факторы, влияющие на уровень заболеваний, и моделируется распространение эпидемий. Пространственно распределенные данные используются при моделировании запасов полез­ных ископаемых и рыбных ресурсов, социально-экономической, криминогенной ситуации и природных катастроф (оползней, лавин и пр.).

Глубокий анализ и моделирование пространственных данных требуют при­менения комплексного подхода и различных методов, характеризующих ту или иную особенность явления. Сложность такого анализа обусловлена не­сколькими факторами: наличием больших объемов количественной и каче­ственной информации по исследуемому явлению, многомасштабностью и многопеременностью, наличием различных факторов влияния.

2. Постановка задачи пространственного анализа

При работе с пространственными данными обычно имеется некоторое ко­личество измерений изучаемой переменной в различных точках, число ко­торых ограниченно. Итак, есть область, на которой проведен ряд измерений некоторой величины Z. Эти измерения проведены в произвольно распределенном по области наборе точек (х, у), которые мы будем называть сетью мониторинга (рис. 1). Но есть и участки области, не покрытые измере­ниями, о значениях величины Z в которых хотелось бы получить информа­цию. Наиболее часто требуется оценить значение наблюдаемой величины в непромеренной точке X на основе имеющихся данных, т. е. решить задачу интерполяции.

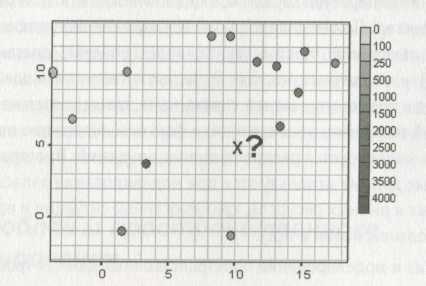
Рис. 1 Постановка задачи пространственного оценивания

Данные измерений, как правило, дискретны и пространственно неоднород­но распределены. Анализ данных и его результаты зависят от качества и количества исходных данных, от методов и моделей обработки данных.

Перечень конкретных задач, для решения которых необходимо применение комплекса исследований с помощью методов геостатистики - т.е. статистики пространственно распределенной информации:

1. оценить значение в точке, где измерение не проводилось;

2. нарисовать карту, построить изолинии (определить значения на плот­ной сетке);

3. оценить ошибку интерполяционной оценки;

4. оценить значение переменной, по которой мало измерений, используя значения другой коррелированной с ней переменной, по которой про­ведено много измерений;

5. определить вероятность того, что значения наблюдаемой переменной превысят заданный уровень в интересующей нас области;

6. получить набор равновероятных стохастических пространственных реа­лизаций распределения наблюдаемой переменной.

Первые три задачи — примеры задач регрессии или классификации (в за­висимости от типа исходных значений). Две последние задачи относятся к вероятностному анализу и связаны с оценками риска.