Задачи и упражнения iiIго типа.
Задача №1.
Максимально упростите выражения своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.
![]()
(Отметим эту функцию как F1, для таблицы истинности)
Решение:
1) Максимально упростим выражение.
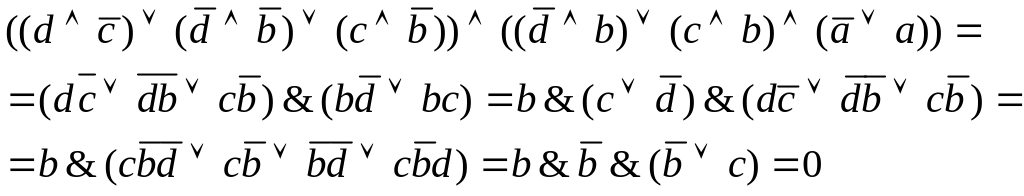
(Отметим эту функцию как F2, для таблицы истинности)
2) Строим таблицу истинности.
а |
b |
c |
d |
f2 |
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
f1 x6&x7 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
Из таблицы истинности видно, что значения функции F1 и F2 на всех наборах переменных совпадают. Это значит, что упрощение исходного выражения было верным и F2=F1.
Задача №2.
Аналитическим способом, т.е. на основе формул взаимосвязи между
логическими
операциями, докажите справедливость
ниже приведенных тождеств. Затем с
помощью диаграмм Эйлера – Венна
подтвердите справедливость этого
доказательства; представьте одно из
выражений (предварительно его упростив)
в базисе элементарных функции. В наборе
номеров базисных функции должны
фигурировать цифры вашего варианта.
Например, для варианта 12 могут быть
взяты следующие функции:![]() ,
,![]() ,
,
![]() .
Недостающие функции отбираются на
основе теории классов.
.
Недостающие функции отбираются на
основе теории классов.
((a– d) (a ~ d)) – ((b – c) (b ~ c)) = ((b d) (a | b)) ((c d) | (a c))
Решение:
Докажем справедливость данных тождеств.
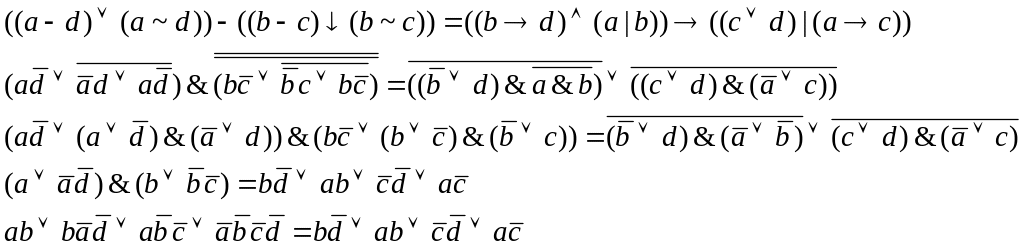
2) Строим диаграммы Эйлера-Венна.
Левая часть: |
Правая часть: |
A
C
D
U
B |
A
C
B
D
U |
=> тождество справедливо.
3) Представим одно из выражений в базисе элементарных функции
![]()
Таблица истинности:
x1 |
x2 |
f1 |
f11 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Проверка на принадлежность к классам Поста:
P0:
![]()
![]()
![]()
![]()
P1:
![]()
![]()
![]()
S:
![]() ,
,
![]()
![]() ;
;
,
![]() ;
;
M:
![]()
![]()
![]()
L:
![]() - нелинейная;
- нелинейная;
![]() -
нелинейная;
-
нелинейная;
|
P0 |
P1 |
S |
M |
L |
f1 |
+ |
+ |
- |
+ |
- |
f11 |
- |
+ |
- |
- |
- |
Недостающая
функция
![]() :
:
-
P0
P1
S
M
L
-
+
+
-
+
представим выражение
в {![]() ,
,
![]() }
– базисе.
}
– базисе.
![]()
Задача №3.
Воспользовавшись таблицами истинности, представьте логические выражения вашего варианта двух последних заданий в СПНФ. Затем произведите минимизацию методом карт Карно (результаты расчета проверьте с помощью таблиц истинности). Наконец, определите, к каким классам (P0, P1, S, M, L) относятся ваши логические выражения.
Решение:
1) Строим таблицу истинности.
![]()
![]() .
.
-
A
b
c
d
f1
f2
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
0
0
1
1
0
0
0
1
0
0
0
1
0
1
0
1
0
0
0
1
1
0
0
0
0
1
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
1
1
0
1
0
0
0
1
0
1
1
0
0
1
1
0
0
0
1
1
1
0
1
0
1
1
1
1
0
0
1
1
1
1
1
0
1
f1:
![]()
![]()
f2:
![]()
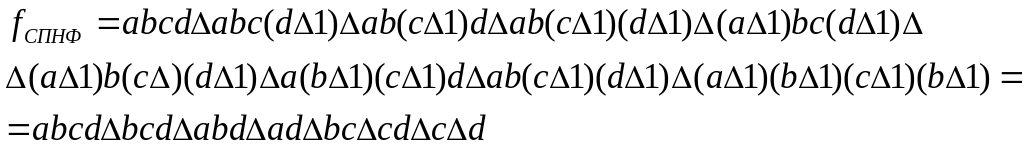
Минимизируем методом карт Карно.
Функция f1=0 поэтому ее некорректно рассматривать в данном задании.
f2:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
3) Проверка на принадлежность к классам Поста:
P0:
![]()
![]()
P1:
![]()
![]()
S:
![]()
![]()
![]()
![]()
![]()
M:
![]()
![]()
L:
![]() - линейная;
- линейная;
![]() - нелинейная.
- нелинейная.
|
P0 |
P1 |
S |
M |
L |
f1 |
+ |
- |
+ |
- |
+ |
f2 |
- |
+ |
- |
- |
- |
Задача №4.
Докажите аналитическим путем справедливость трех предложенных выражений в каждом варианте.
1. ((A
![]()
![]() )
)
![]() (
C))
((
(
C))
((![]() B)
(B
B)
(B
![]() ))
= 0;
))
= 0;
(A – (B – C))
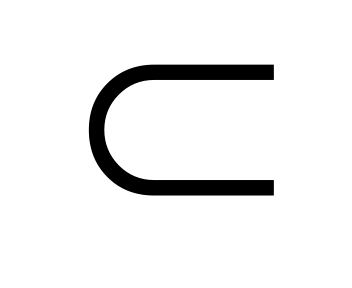 (A
(B
C));
(A
(B
C));(b (a c)) ((b c) a) = b a.
Решение:
1.
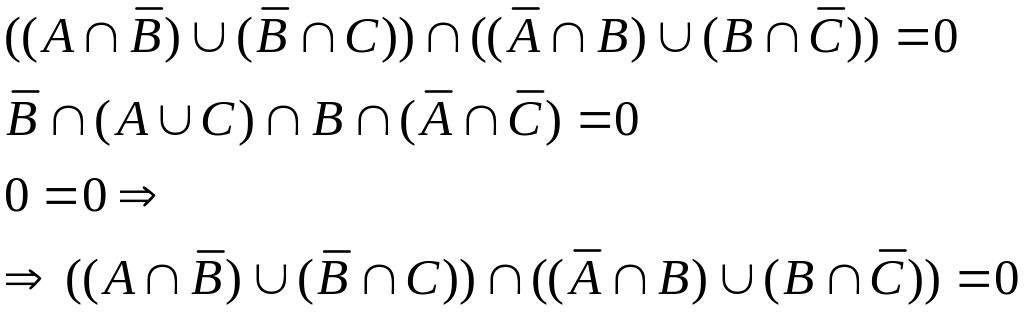
2.

3.![]()
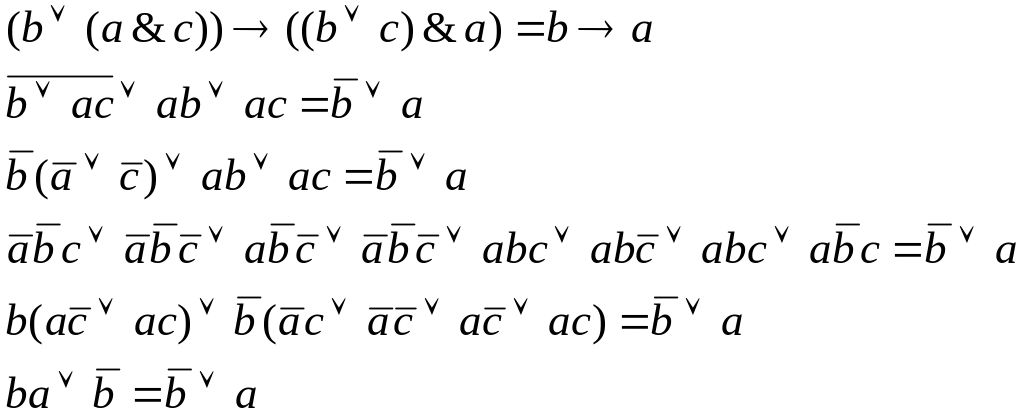
Задача №5.
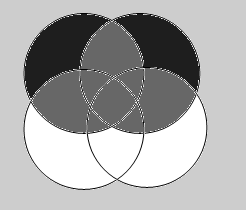
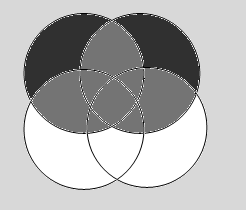
Ниже приведены диаграммы Эйлера – Венна. Представьте заштрихованные и отдельно не заштрихованные области максимально компактными аналитическими выражениями, в которых бы использовалось минимальное количество логических операций и букв. С этой целью сначала выразите все заштрихованные области через конституенты – конъюнкты, а незаштрихованные через конституенты – дизъюнкты, и только после этого приступаете к упрощению совершенных форм (результаты проверьте на таблицах истинности).
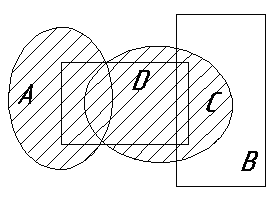
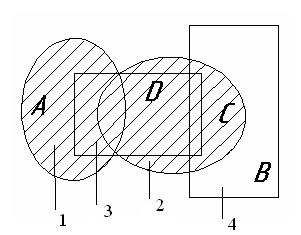
Выразим все заштрихованные области :
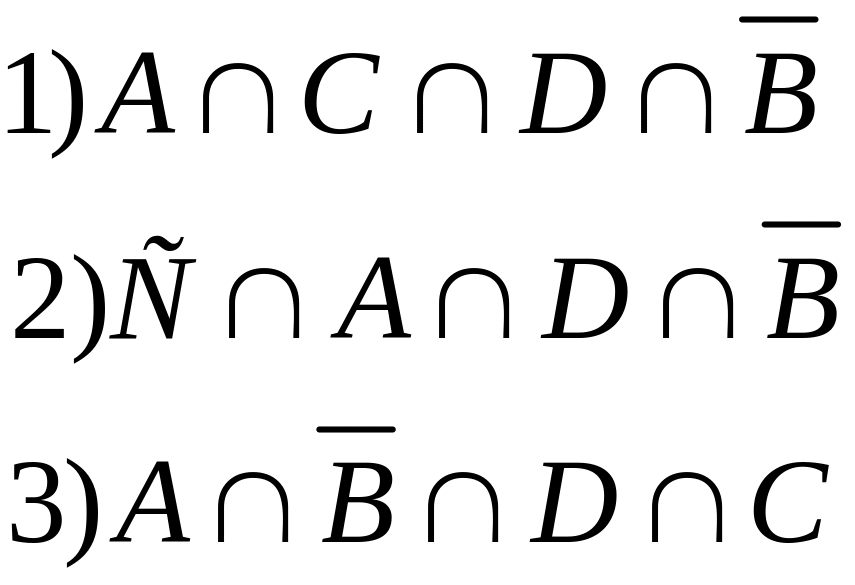
Строим таблицу истинности:
A |
b |
c |
d |
|
|
|
|
f1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Построим минимизирующие карты:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
![]()
Строим таблицу истинности:
A |
b |
c |
d |
|
|
|
|
f2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Выразим не заштрихованные области:
![]()
![]()
Строим таблицу истинности:
A |
b |
c |
d |
|
|
|
|
f1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
1 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
![]()
A |
b |
c |
d |
|
|
|
|
f2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Вывод
В ходе выполнения работы мы мы освоили навыки решения задач, с помощью функций алгебры логики, выполняя задачи типа I, II, III.