3.2 Геометрическое представление фал.
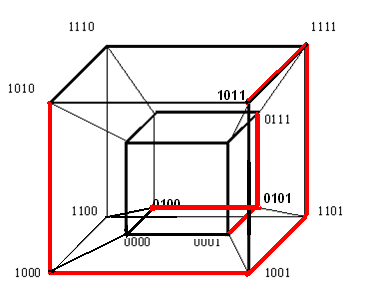
Если наборам значений аргументов функции алгебры логики сопоставлять точки n-мерного пространства, то множество 2n наборов определяет множество вершин n-мерного единичного куба.
3.3 Найдем сднф и скнф.
=
Задача №4. Определить принадлежность к классам Поста (воспользуемся функцией из предыдущего упражнения).
Решение:
Проверка на принадлежность к классам Поста:
P0-класс функций, сохраняющих константу ноль.
(0,0,0,0)=0
P0;
P1- класс функций, сохраняющих константу единица.
(1,1,1,1)=0;
P1;
S- класс самодвойственных функций.
Функция называется самодвойственной, если она совпадает с двойственной себе функцией, т. е. имеет место равенство: = .
(0,0,0,1)=1;
S.
M -класс монотонных функций.
Функция называется монотонной, если для любых двух наборов и , таких, что , имеет место равенство: .
M.
Данная функция не принадлежит классу монотонных функций, так как значение функции (0,1,1,0) (0,0,1,1), а набор (0,1,0)<(0,1,1). Для любых двух наборов и , таких, что , не выполняется равенство: .
L -класс линейных функций.
Функция называется линейной, если она представима в следующем виде: , где коэффициенты , {0,1}, = .
=f(0,0,0,0)=0
= f(1,0,0,0)=0 1=1
= f(0,1,0,0)=0 1=1
= f(0,0,1,0)=0 0=0
=
f(0,0,0,1)=0
1=1
(
a,b,c,d
) =
a
b
c
d
=0
1a
1b
0c
1d=0
a
.
a |
b |
c |
d |
a |
f(a,b,c,d) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0
a
- нелинейная.
|
P0 |
P1 |
S |
M |
L |
(a,b,c,d) |
+ |
- |
- |
- |
- |
Задача №5. Построить функционально полную систему функции так, чтобы эта система была базисом и содержала .
=z
p
y
z
x
p
y
z/¬x
Решение:
1) Рассмотрим функцию в булевом базисе:
2) Составим таблицу истинности:
-
x
y
z
p
f
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
1
0
1
1
1
1
1
0
0
1
1
1
0
1
1
1
1
1
0
1
1
1
1
1
1
3) Проверка на принадлежность к классам Поста:
P0:
P1:
S:
,
M:
L: =f(0,0,0,0)=1
= f(1,0,0,0)=1 1=0
= f(0,1,0,0)=1 0=1
= f(0,0,1,0)=1 0=1
= f(0,0,0,1)=1 0=1
( x,y,z,p ) = x y z p =1 0x 1y 1z 1p=1 y z p.
Построим таблицу истинности:
y |
z |
p |
(1) |
(2) |
(3) |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
Функция нелинейна.
-
P0
P1
S
M
L
-
+
+
-
-
4) Недостающая
функция
:
-
P0
P1
S
M
L
+
-
-
-
+
5) Функционально полная система, которая является базисом:
{f(x,y,z,p),
}.