9

ЛАБОРАТОРНА РОБОТА №1

РОЗРОБЛЕННЯ ЗАСТОСУВАННЯ ДЛЯ ВІЗУАЛІЗАЦІЇ СТАТИСТИЧНИХ ДАНИХ ТА ОБЧИСЛЕННЯ ХАРАКТЕРИСТИК ВАРІАЦІЙНОГО РЯДУ

Мета роботи: Вивчення методів візуалізації статистичних даних, обчислення характеристик варіаційного ряду та розробки відповідного програмного забезпечення.

1. КЛЮЧОВІ ПОЛОЖЕННЯ

Математична статистка – науковий напрямок, в межах якого розробляються методи систематизації, аналізу та використання статистичних даних для отримання наукових та практичних висновків. В основу математичної статистики покладено теорію ймовірностей переважно для того, щоб оцінювати надійність та точність висновків, що отримують на підґрунті аналізу обмежених статистичних даних. Наприклад, яка кількість статистичних даних необхідна для того, щоб отримати надійні висновки на основі їх аналізу.

Першою задачею статистики є встановлення способів збирання та угрупування статистичних даних. Нехай необхідно дослідити сукупність однорідних явищ, об’єктів чи процесів відносно деякої знаки, яка може бути якісною або кількісною. Наприклад, якщо є партія апельсинів, то якісною ознакою може бути певна характеристика зовнішнього вигляду апельсину, а кількісною – його вага.

Для того щоб зробити висновок відносно обраної ознаки можна виконати обслідування всіх об’єктів. На практиці, зважаючи на значну кількість об’єктів, повне обслідування практично не застосовується. Найбільш прийнятним способом є відбір з усієї множини об’єктів певної обмеженої сукупності, об’єкти якою потім обслідують.

Вибірковою сукупністю, або просто вибіркою, називають сукупність об’єктів відібраних випадковим чином.

Генеральною сукупністю називають множину об’єктів, з яких здійснюється вибірка.

Обсягом сукупності (генеральної чи вибіркової) називають кількість об’єктів у цій сукупності.

При складанні вибірки можливі два підходи, а саме: після того як об’єкт відібраний та обслідуваний, його повертають або не повертають у генеральну сукупність. У зв’язку з цим розрізняють вибірки з повторенням або без повторення.

Вибіркою з повторенням називають сукупність, у якій відібраний об’єкт перед вибором наступного повертається у генеральну сукупність.

Вибіркою без повторень називають сукупність, у якій обраний об’єкт не повертається у генеральну сукупність.

Для того щоб по даним вибірки можна було зробити достатньо обґрунтовані висновки стосовно обраної ознаки об’єктів генеральної сукупності, необхідно щоб вибірка точно відображала особливості генеральної сукупності. Якщо ця умова виконується, то вибірку називають репрезентативною. Одним із способів формування репрезентативної вибірки є спосіб, коли об’єкти з генеральної сукупності відбираються випадковим чином, так щоб ймовірність потрапити у вибірку для кожного об’єкта була однаковою.

При формуванні вибірки використовується просте випадкове відбирання з усієї генеральної сукупності і відбирання при якому генеральна сукупність поділяється на частини. Наприклад, для того щоб провести опитування з метою з’ясування попиту на нову послугу можна випадковим чином сформувати з генеральної сукупності вибірку без урахування, наприклад, віку користувачів, або поділити генеральну сукупність на певні вікові категорії та з кожної такої категорії сформувати вибірки. У першому випадку спосіб формування вибірки називають простим випадковим відбиранням, а у другому випадку – типізованим відбиранням. Типізоване відбирання доцільно використовувати у тих випадках коли досліджувана ознака генеральної сукупності суттєво відрізняється у кожній категорії або групі.

Нехай, у вибірці, що отримана з генеральної сукупності, значення ознаки спостерігалось раз, - раз, - раз, а обсяг вибірки . Значення прийнято називати варіантами, а послідовність варіант опорядкованих у порядку зростання – варіаційним рядом. Число спостережень варіанти називають частотою, а відношення − відносною частотою.

Статистичним розподілом вибірки називають перелік варіант та відповідних їм частот. Статистичний розподіл можна задати також у вигляді послідовності інтервалів та відповідних їм частот, при цьому частоту визначають як кількість значень, що належать цьому інтервалу.

Нехай відомо статистичний розподіл частот ознаки . Позначимо через частоту спостереження варіант, що задовольняють умові . Очевидно, що .

Тоді відносна частота події буде дорівнювати .

Для різних значень отримаємо різні значення відносних частот . Залежність від , що встановлюють дослідним (емпіричним) способом, називають емпіричною функцією розподілу відносних частот.

Розглянемо приклад. У табл. 1 наведені значення варіант їх частоти.

Таблиця 1 – Дослідні дані

№
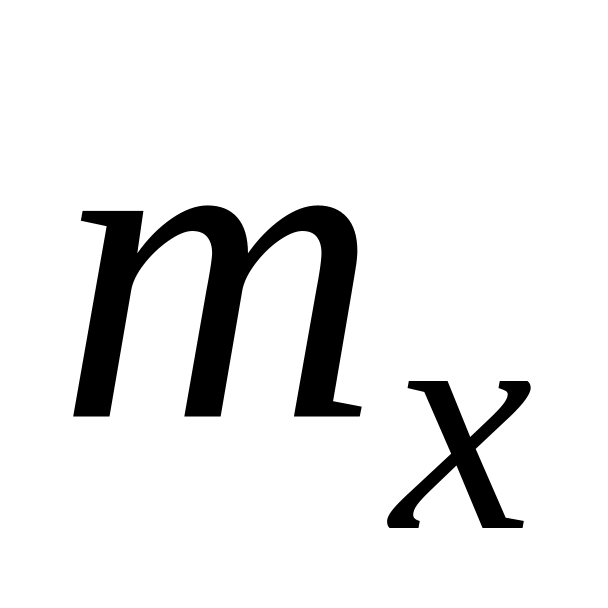
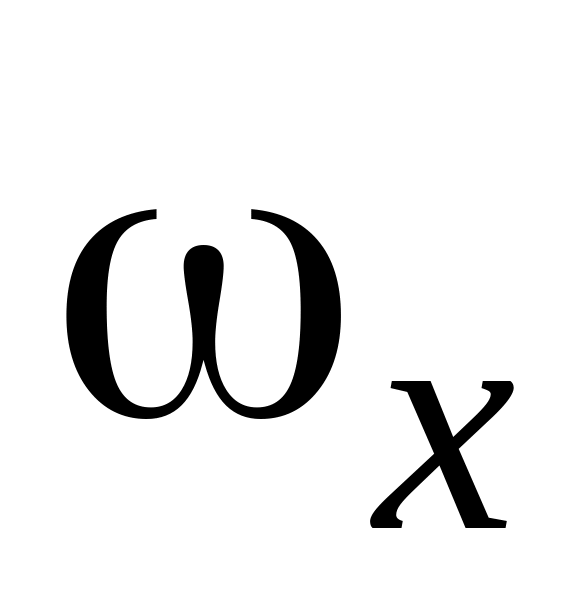
1	3	5	5	0,018
2	4	12	17	0,062
3	5	16	33	0,120
4	6	18	51	0,168
5	7	21	72	0,263
6	8	34	106	0,387
7	9	45	151	0,551
8	10	40	191	0,697
9	11	32	223	0,814
10	12	24	247	0,901
11	13	15	262	0,956
12	14	10	272	0,993
13	15	2	274	1

Обсяг вибірки . Наприклад, для :

.

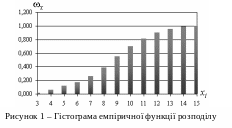
Для того, щоб візуалізувати отримані результати можна побудувати гістограму (рис.1,2).

С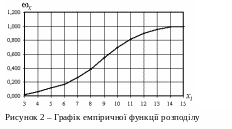 тосовно генеральної сукупності, якщо вважати що її обсяг , функцію розподілу називають теоретичною функцією розподілу ймовірностей. Генеральна сукупність може характеризуватись також і теоретичною функцією розподілу щільності ймовірностей.

Д ля вибірки можна побудувати емпіричну функцію щільності частот. Гістограма цієї функції наведена на рис. 3.

Після того як побудовані емпіричні функції можна зробити висновок стосовно теоретичних функцій генеральної сукупності та встановити їх параметри. Наприклад, якщо стало відомо, що досліджувана ознака генеральної сукупності підкоряється нормальному розподілові, то можна отримати оцінку (найти приблизне значення) математичного очікування та дисперсії, оскільки ці два параметри цілком визначають нормальний розподіл ймовірностей. Оцінку параметрів статистичного розподілу можна отримати використовуючи переважно вибіркові дані. Розглянемо основні параметри статистичних розподілів.

Вибіркове та ганеральне середнє.

Нехай з генеральної сукупності отримано відносно деякої ознаки отримано вибірку обсягу . Вибірковим середнім називають середньоарифметичне значення ознаки вибіркової сукупності. Якщо всі значення ознаки різні, то

.

У випадку, коли у вибірці значення мають відповідні частоти , такі що , то вибіркове середнє обчислюється за формулою

.

Очевидно, що вибіркове середнє, обчислене по одній вибірці буде відрізнятись від вибіркового середнього обчисленого по другій вибірці. Таким чином вибіркове середнє необхідно розглядати як випадкову величину. Не зважаючи на це можна показати, що у випадку коли вибіркові сукупності та генеральна сукупність мають однакові статистичні розподіли, то вони мають приблизно однакові середні значення. Якщо обсяг вибірки збільшується, то вибіркове середнє прямує до генерального середнього.

Якщо перед формуванням вибірки генеральну сукупність було поділено на групи, то у цьому випадку обчислюється групове та загальне вибіркові середні значення.

Груповим середнім називають середньоарифметичне значення ознаки в межах групи.

Спільним середнім називають середньоарифметичне значення ознаки для всієї вибірки. Нехай деяка вибіркова сукупність містить груп обсягом . Для кожної групи відомо групові середні . Спільне середнє можна знайти за формулою

.

Вибіркова та генеральна дисперсії

Для того щоб охарактеризувати розсіювання значень досліджуваної ознаки відносно середнього значення, використовується параметр ститистичного розподілу який називається дисперсія.

Під генеральною дисперсією розуміють середньоарифметичне квадратів відхилень значень ознаки від їх середнього . Якщо всі значення ознаки генеральної сукупності обсягом різні, то

.

Якщо значення спостерігаються у генеральній сукупності з частотами , то

.

Крім дисперсії для характеристики розсіювання значень відносно використовують також середньоквадратичне відхилення

.

Аналогічним чином розраховуються вибіркова дисперсія та вибіркове середньоквадратичне відхилення :

,

,

.

Тут - вибіркові значення, - частоти вибіркових значень, - обсяг вибірки.

Для обчислення дисперсії можна скористатись спрощенною формулою. Для цього перепишемо вираз для обчислення дисперсії

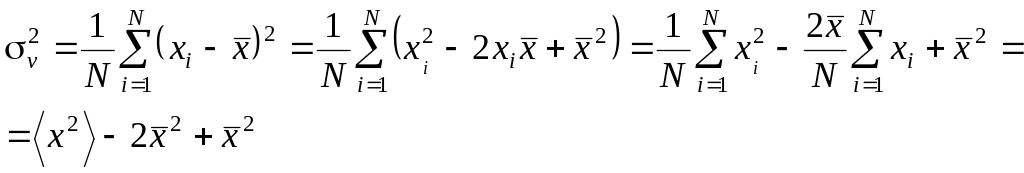
Остаточно

.

Тут - середнє значення квадратів значень ознаки.

Групова, внутрішньогрупова, міжгрупова та спільна дисперсії

Якщо генеральна сукупність поділена на напересічні групи, то для характеристики розсіювання значень ознаки, що належать групі використовують групову дисперсію. Нехай генеральна сукупність поділена на груп: к , де - обсяг -ї групи. Тоді групова дисперсія обчислюється за формулою

,

де - частота -го значення у - й групі.

Внутрішньогрупова дисперсія розраховується, як зважене середнє групових дисперсій

,

де - обсяг генеральної сукупності.

Міжгруповою дисперсією називають зважену дисперсію групових середніх відносно спільного середнього .

.

Спільною дисперсією називають дисперсію ознаки генеральної сукупності відносно спільного середнього

.

2. КЛЮЧЕВЫЕ ВОПРОСЫ

1. Наведіть визначення генеральної та вибіркової сукупностей?

2. Способи формування вибіркових сукупностей.

3. Що таке варіаційний ряд?

4. Емпірична й теоретична функції статистичного розподілу.

5. Вибіркові, групові та загальні середні.

6. Групові дисперсія та середнє квадратичне відхилення.

7. Внутрішньогрупова, міжгрупова та загальна дисперсії.

3. ДОМАШНЕЕ ЗАДАНИЕ

Згідно варіанту завдання:

1. Побудувати гістограми емпіричної функції статистичного розподілу та гістограму емпіричної щільності вірогідності.

2. Розрахувати статистичні ознаки варіаційних рядів (групові середні, дисперсії та середні квадратичні відхилення).

3. Розрахувати загальнє середнє, внутрішньогрупову, міжгрупову та загальну дисперсії.

4. ЛАБОРАТОРНЕ ЗАВДАННЯ

Згідно варіанту завдання:

1. Скласти програмне застосування для візуалізації статистичних даних та обчислення статистичних ознак варіаційних рядів.

Вимоги до програми:

1. написання на мові програмування С++;

2. наявність графічного інтерфейсу користувача, що надає змогу вводу й виводу вихідних даних;

3. використання варіаційних рядів довільної довжини.

5. ВАРІАНТИ ЗАВДАНЬ

Варіант завдания обирається згідно номеру бригады з таблиці:

Variant	X	P1	P2	P3	Variant	X	P1	P2	P3
1	0	18	1	1	2	0	3	38	1
	1	16	1	2		2,5	6	33	2
	2	15	2	4		5	14	29	2
	3	13	3	8		7,5	31	26	4
	4	12	4	13		10	61	23	5
	5	11	6	23		12,5	114	20	8
	6	10	9	37		15	200	18	13
	7	9	13	56		17,5	327	16	19
	8	8	19	81		20	501	14	29
	9	7	27	113		22,5	720	12	45
	10	7	39	148		25	968	11	68
	11	6	56	186		27,5	1218	9	104
	12	5	80	221		30	1436	8	159
	13	5	115	251		32,5	1585	7	243
	14	4	166	270		35	1638	7	371
	15	4	239	277		37,5	1585	6	566
	16	4	345	270		40	1436	5	864
	17	3	496	251		42,5	1218	4	1318
	18	3	345	221		45	968	4	2011
	19	3	239	186		47,5	720	3	3069
	20	2	166	148		50	501	3	4682
	21	2	115	113		52,5	327	3	3069
	22	2	80	81		55	200	2	2011
	23	2	56	56		57,5	114	2	1318
	24	2	39	37		60	61	2	864
	25	1	27	23		62,5	31	2	566
	26	1	19	13		65	14	1	371
	27	1	13	8		67,5	6	1	243
	28	1	9	4		70	3	1	159
	29	1	6	2		72,5	1	1	104
3	0	408	1	5	4	0	25	1	941
	5	581	2	5		1,666	22	1	1097
	10	827	4	4		3,333	20	2	1243
	15	1177	7	4		5	18	2	1370
	20	1677	13	4		6,666	16	3	1468
	25	2388	23	4		8,333	14	5	1530
	30	3401	38	4		10	13	6	1552
	35	2388	62	3		11,66	12	8	1530
	40	1677	97	3		13,33	10	11	1468
	45	1177	146	3		15	9	15	1370
	50	827	212	3		16,66	8	21	1243
	55	581	298	3		18,33	7	28	1097
	60	408	403	3		20	7	39	941
	65	286	527	2		21,66	6	52	786
	70	201	665	2		23,33	5	71	638
	75	141	810	2		25	5	96	504
Variant	X	P1	P2	P3	Variant	X	P1	P2	P3
3	80	99	951	2	4	26,66	4	130	387
	85	70	1077	2		28,33	4	176	289
	90	49	1178	2		30	3	239	210
	95	34	1243	2		31,66	3	324	148
	100	24	1265	2		33,33	3	440	102
	105	17	1243	2		35	2	596	68
	110	12	1178	1		36,66	2	808	44
	115	8	1077	1		38,33	2	1095	28
	120	6	951	1		40	2	1485	17
	125	4	810	1		41,66	2	2013	10
	130	3	665	1		43,33	1	2729	6
	135	2	527	1		45	1	3699	3
	140	1	403	1		46,66	1	2729	2
	145	1	298	1		48,33	1	2013	1
5	0	1	11	1	6	0	1	1	3
	0,666	1	10	1		3,333	1	2	3
	1,333	1	9	1		6,666	2	3	3
	2	1	9	1		10	2	4	3
	2,666	2	8	2		13,33	2	7	3
	3,333	2	7	2		16,66	3	10	3
	4	2	7	2		20	4	14	2
	4,666	2	6	2		23,33	4	20	2
	5,333	3	6	2		26,66	5	26	2
	6	3	5	3		30	7	33	2
	6,666	3	5	3		33,33	8	41	2
	7,333	3	4	3		36,66	10	48	2
	8	4	4	4		40	13	55	2
	8,666	4	4	4		43,33	15	60	2
	9,333	4	3	5		46,66	19	63	2
	10	4	3	5		50	24	65	2
	10,66	5	3	6		53,33	29	63	2
	11,33	5	3	6		56,66	36	60	2
	12	5	3	7		60	44	55	2
	12,66	6	2	8		63,33	55	48	1
	13,33	6	2	9		66,66	68	41	1
	14	6	2	10		70	84	33	1
	14,66	6	2	11		73,33	103	26	1
	15,33	7	2	12		76,66	103	20	1
	16	7	2	14		80	84	14	1
	16,66	7	1	15		83,33	68	10	1
	17,33	7	1	17		86,66	55	7	1
	18	7	1	19		90	44	4	1
	18,66	7	1	21		93,33	36	3	1
	19,33	7	1	24		96,66	29	2	1
7	0	4	42	7	8	0	1	18	160
	2,666	3	55	12		10	1	16	170
	5,333	3	71	21		20	1	15	177
	8	3	93	35		30	2	13	181
	10,66	3	122	55		40	2	12	183
Variant	X	P1	P2	P3	Variant	X	P1	P2	P3
7	13,33	3	159	82	8	50	2	11	181
	16	3	207	118		60	3	10	177
	18,66	3	270	161		70	4	9	170
	21,33	3	270	211		80	4	8	160
	24	2	207	263		90	5	7	148
	26,66	2	159	312		100	6	7	135
	29,33	2	122	353		110	7	6	122
	32	2	93	381		120	9	5	107
	34,66	2	71	393		130	11	5	93
	37,33	2	55	386		140	13	4	79
	40	2	42	362		150	15	4	67
	42,66	2	32	323		160	19	4	55
	45,33	2	25	275		170	22	3	45
	48	2	19	224		180	27	3	36
	50,66	2	14	173		190	32	3	28
	53,33	1	11	128		200	39	2	22
	56	1	8	90		210	46	2	16
	58,66	1	6	61		220	56	2	12
	61,33	1	5	39		230	67	2	9
	64	1	4	24		240	80	2	7
	66,66	1	3	14		250	96	1	5
	69,33	1	2	8		260	80	1	3
	72	1	2	4		270	67	1	2
	74,66	1	1	2		280	56	1	2
	77,33	1	1	1		290	46	1	1
9	0	1	442	21	10	0	16	93	32
	8,333	1	457	18		6,666	14	115	33
	16,66	2	464	17		13,33	13	142	34
	25	2	464	15		20	12	175	34
	33,33	3	455	14		26,66	11	195	35
	41,66	4	438	12		33,33	10	158	34
	50	5	416	11		40	9	128	34
	58,33	6	387	10		46,66	8	103	33
	66,66	8	354	9		53,33	7	84	31
	75	11	319	8		60	7	68	30
	83,33	14	282	7		66,66	6	55	28
	91,66	18	245	7		73,33	6	44	26
	100	24	209	6		80	5	36	24
	108,3	31	175	5		86,66	5	29	21
	116,6	40	145	5		93,33	4	24	19
	125	52	117	4		100	4	19	17
	133,3	68	93	4		106,6	3	15	15
	141,6	88	73	3		113,3	3	13	13
	150	115	56	3		120	3	10	11
	158,3	88	43	3		126,6	3	8	9
	166,6	68	32	3		133,3	2	7	8
	175	52	23	2		140	2	5	7
	183,3	40	17	2		146,6	2	4	5
	191,6	31	12	2		153,3	2	4	4
Variant	X	P1	P2	P3	Variant	X	P1	P2	P3
9	200	24	8	2	10	160	2	3	4
	208,3	18	6	2		166,6	1	2	3
	216,6	14	4	1		173,3	1	2	2
	225	11	2	1		180	1	2	2
	233,3	8	2	1		186,6	1	1	1
	241,6	6	1	1		193,3	1	1	1