
Порядок виконання роботи
Ввімкнути тумблер звукового генератора, який живиться від мережі U=220 В.
Опустити мікрофон вниз до відказу.
Повільно обертаючи ручку блока, поволі піднімати мікрофон. При цьому гучність звучання буде періодично посилюватись та слабнути. Слід фіксувати по шкалі такі положення l0, l1, l2… мікрофона, коли гучність звучання максимальна. Кожне положення мікрофона, що відповідає резонансу, визначити 3-4 рази і знайти середнє значення.
Обчислити середню відстань між двома сусідніми максимумами.
За формулою 2.12 визначити довжину хвилі у повітрі.
Записати значення частоти звукових коливань, які подаються за допомогою генератора і за формулою (2.2) визначити швидкість звуку в повітрі при кімнатній температурі.
Використовуючи вираз
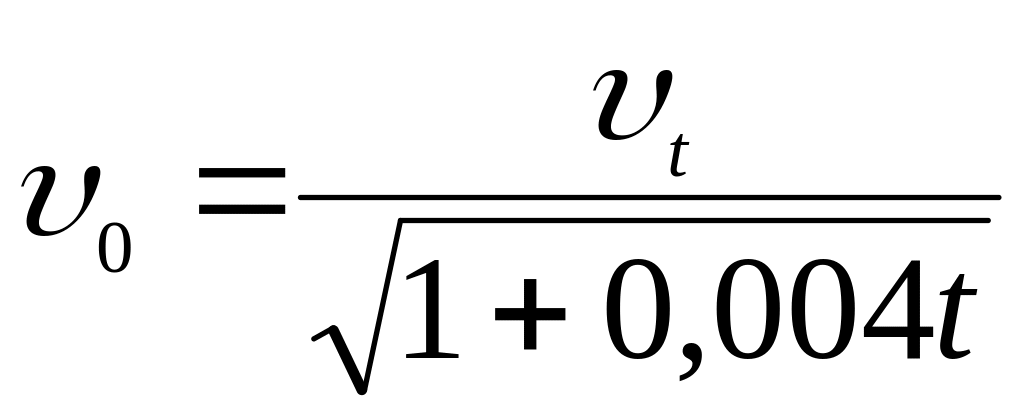 (2.13) обчислити швидкість υ0
звуку при t=0
0С.
(2.13) обчислити швидкість υ0
звуку при t=0
0С.Дані вимірів занести до таблиці 2.1.
Таблиця 2.1
Номер досліду |
l0 |
l1 |
l2 |
l3 |
l4 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
lсер |
|
|
|
|
|
l1-l0 |
l2-l1 |
l3-l2 |
l4-l3 |
∆lсер |
λ |
|
|
|
|
|
|
Швидкість звуку при кімнатній температурі: υt =
швидкість звуку при t=0 0С: υ0 =
Питання для самоперевірки
Дайте визначення звуку, ультразвуку, інфразвуку. Звукові хвилі якої частоти сприймає вухо людини?
Запишіть та поясніть рівняння прямої та відбитої біжучих хвиль.
Що називається стоячею хвилею? Які умови її виникнення?
Запишіть та поясніть рівняння стоячої хвилі.
Яким умовам задовольняють координати вузлів та пучностей у стоячій хвилі?
Яка відстань між сусідніми вузлами, пучностями, вузлом та пучністю?
Коли виникає явище звукового резонансу в трубах?
Який вигляд має стояча хвиля, що відповідає основному тону у закритій з одного боку трубі? У відкритій з обох боків трубі?
Як залежить від температури швидкість звуку в повітрі?
Лабораторна робота № 3 визначення відношення питомих теплоємностей газів
Мета роботи: вивчити перший закон термодинаміки, експериментально визначити показник адіабати.
Т еоретичні відомості
Експериментальна установка (рис. 2.1) складається зі скляного балона 1 достатньо великої ємності, сполученого з рідинним U-подібним манометром 2. Верхня частина балона закрита кришкою на якій знаходяться крани 3 і 4, за допомогою яких балон сполучається з атмосферою, і джерелом тиску 5 (у даному випадку гумовою грушею) або насосом.
Нехай у балоні спочатку був атмосферний тиск. Якщо швидко підвищити тиск у балоні і закрити кран 4, то остаточна різниця рівнів у манометрі h1 встановиться не відразу (при швидкому стиску температура газу в балоні підвищиться і пройде якийсь час, поки температура повітря в балоні не зрівняється за рахунок теплопровідності з температурою навколишнього повітря). Позначимо температуру навколишнього повітря Т0, а через Р1 –тиск газу усередині балона, що відповідає сталому показанню манометра h1. Якщо Ра – атмосферний тиск, то
Р1 = Ра + h1 (2.1)
При цьому Ра і h1 повинні мати однакову розмірність. Назвемо першим (I) станом стан газу, що характеризується параметрами Р1 і Т0.
Якщо тепер швидко відкрити кран 3, то повітря буде адіабатично розширюватися до атмосферного тиску і при цьому охолоне до температури Т2. Параметрами Ра і Т2 буде визначатися другий (II) стан газу.
Якщо після відкривання крана 3 і вирівнювання тиску його знову закрити, то повітря в балоні, що охололо при адіабатичному розширенні, знову нагріється в ізохоричному процесі до температури навколишнього середовища Т0 і тиск зросте до величини Р2, що відповідає сталому показанню манометра h2
Р2 = Ра + h2 (2.2)
Параметрами Р2 і Т0 буде визначатися третій (III) стан газу.
Отже, ми маємо три стани газу, що характеризуються такими параметрами:
I стан – Т0, Ра + h1;
II стан – Т2, Ра; (2.3)
III стан – Т0, Ра + h2.
Розглядаючи газ як ідеальний, за допомогою рівнянь адіабатичного і ізохоричного процесів запишемо вирази, що зв'язують параметри газу в трьох станах:
адіабатичний процес (перехід із стана
I у стан II):
![]() (2.4)
(2.4)
ізохоричний
процес (перехід із стана
II у стан
III:
![]() (2.5)
(2.5)
Розділивши рівняння (2.4) на (2.5), після перетворень отримаємо
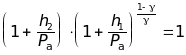 (2.6)
(2.6)
Прологарифмуємо цей вираз і одержимо розрахункову формулу методу:
![]() (2.7)
(2.7)
