АВІАКОСМІЧНИЙ ЛІЦЕЙ

НАЦІОНАЛЬНОГО АВІАЦІЙНОГО УНІВЕРСИТЕТУ

РОБОЧИЙ ЗОШИТ

для лабораторного практикуму з фізики

учня (учениці) _____групи

__________________________________________

_________________________________________

_________________________________________

Київ

Лабораторна робота № 1

КОЛИВАННЯ ФІЗИЧНОГО МАЯТНИКА

Мета роботи: вивчити закономірності затухаючих механічних коливань фізичного маятника, визначити характеристики таких коливань

Теоретичні відомості

Фізичним маятником зветься тверде тіло, яке має можливість коливатися під дією вла­с­ної ваги біля нерухомої горизонтальної осі О, що не проходить крізь його центр іне­р­ції (рис. 1.1).

У положенні рівноваги центр іне­р­ції маятника знаходиться під точкою підвісу О на вертикальній лінії. Якщо відхилити фізичний маятник від положення рівноваги на кут , то виникне момент сили ваги маятника, який повертає його до положення рівноваги.

Основний закон обертального руху твердого тіла в механіці в узагальненій формі має вигляд

(1.1) де – час, – вектор моменту імпульсу тіла, – вектор моменту сил, які діють на тіло.

У наближенні малих відхилень, при яких , при врахуванні тільки сили ваги, диференціальне рівняння (1.1) дає рівняння руху маятника у вигляді гармонічних коливань:

, (1.2)

де – амплітуда коливань, – циклічна частота власних коливань маятника, – початкова фаза, . Період цих коливань є (1.3) де J – момент інерції маятника відносно осі О, g – прискорення вільного падіння, m – маса маятника, l – відстань ОС.

Якщо тіло маятника побудовано так, що його маса зосереджена біля точки С (матеріальна точка з масою m на невагомому підвісі довжиною l), то маятник назива­ється математичним. В цьому випадку J=ml² та період коливань має вигляд

. (1.4)

При врахуванні сил тертя маятника з навколишнім середовищем, які діють проти руху маятника й гальмують його, розв’язок диференціального рівняння (1.1) (коли не дуже великі сили тертя й ) є

(1.5)

де (1.6)

(1.7)

Рівняння руху маятника (1.5) є рівнянням гармонічних коливань із частотою ω та амплітудою A(t), яка зменшується по закону (1.6). При цьому частота ω < ω₀ згідно з формулою (1.7). Приклад вигляду функцій φ(t), A(t) при δ=ln2, ω=2π наведений на рис. 1.2. Зменшення амплітуди коливань обумовлено втратою енергії маятником при виконанні їм роботи проти сил тертя. Коефіцієнт затухання δ=1/τ визначає швидкість зменшення амплітуди, а проміжок часу τ, за який амплітуда зменшується у e разів називається часом релаксації. Період затухаючих коливань не дорівнює Т₀, він визначається виразом:

(1.8)

Добуток коефіцієнта затухання на період коливань β=δТ називається логарифмічним декрементом затухання. Він задовольняє виразу (1.9)

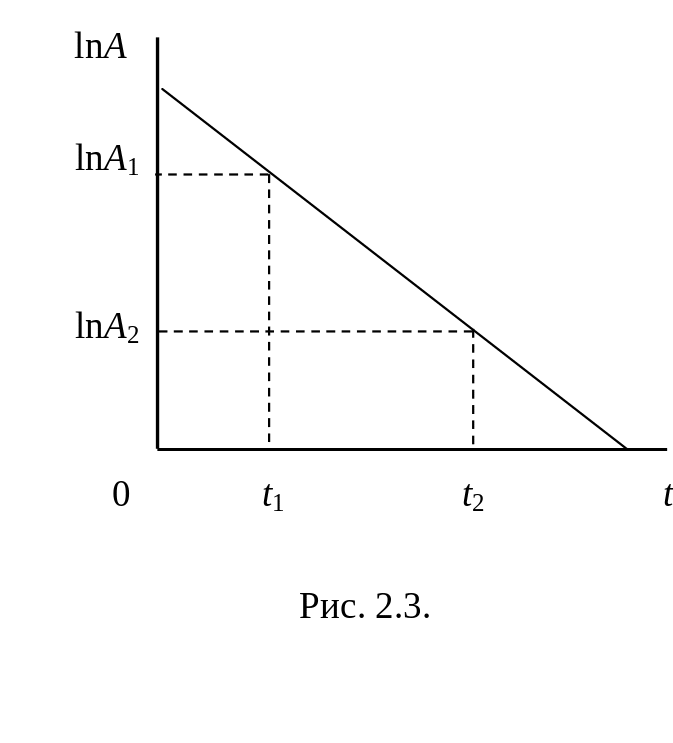
Вираз (1.6) може бути представленим у вигляді lnA(t)=lnA₀ – δt. (1.10)

Рівняння (1.10) є рівнянням прямої лінії у координатах lnA – t, а коефіцієнт

(1.11) визначає нахил цієї прямої лінії до осі часу (рис. 1.3). Ця формула може бути використана для експериментального визначення коефіцієнта затухання якщо виміряна залежність амплітуди від часу. Тоді він дається виразом

(1.12)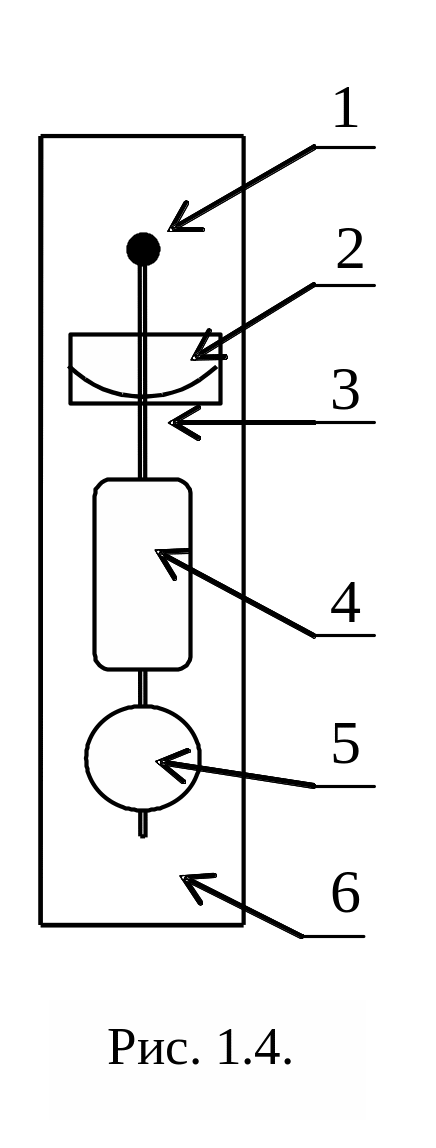

Методика вимірів та лабораторна установка

В роботі використовується фізичний маятник, вигляд якого подається на рис. 1.4. Основою маятника 6 є дошка, закріплена на стіні. До неї віссю 1 приєднаний маятник, виконаний з тонкого металевого підвісу маятника 3 та масивного тіла маятника 5. На підвісі 3 знаходиться повітряне гальмо 4, зроблене у вигляді пластини, яка може обертатися навкруги підвісу 3. Шкала 2 визначає відхилення маятника від положення рівноваги.

Якщо відхилити маятник від вертикального положення, то він починає коливатися у площині, паралельній основі маятника. Швидкість затухання цих коливань визначається орієнтацією пластини повітряного гальма відносно площини коливання. Якщо пластина повітряного гальма паралельна площині коливань (кут α між площиною коливань та пластиною гальма дорівнює нулю), то швидкість затухання коливань мінімальна. В цьому випадку коливання маятника близькі до вільних гармонічних коливань математичного маятника. А при пластині повітряного гальма, розташованій перпендикулярно до площини коливань (α = π/2), відбуваються швидко затухаючі коливання фізичного маятника. Проміжні положення пластини повітряного гальма (0< α < π/2) відповідають різним проміжним значенням затухання коливань.

В даній роботі використовується маятник, для якого δ << ω₀. Тому з великою точністю ω=ω₀.

Амплітуда коливань визначається за шкалою 2, а час – секундоміром.

Порядок виконання роботи

1. Установити положення повітряного гальма з /4.

2. Задатися величиною зменшення амплітуди коливань , рівною 1˚ – 2˚.

3. Відхилити маятник від положення рівноваги на А₀ = 10˚ та відпустити його. Рахуючи число повних коливань маятника від початку коливань послідовно записувати номери коливань N₁, N₂, …, N_n, після яких амплітуда коливань зменшується на k (k – цілі числа 1, 2, …, n ). Це буде відбуватися в моменти часу t_k = N_k <T> (i =1, 2, …, n), які треба обчислити.

4. Результати занести в таблицю 1.1.

5. На графіку з координатними осями lnA – t, використовуючи таблицю 1.1, нанести точки з координатами A _k , t _k . Провести через ці точки пряму лінію. По нахилу цієї лінії визначити коефіцієнт затухання δ та занести його в таблицю 1.1.

6. Повторити пп. 2-5 для положення повітряного гальма з

Таблиця 1.1

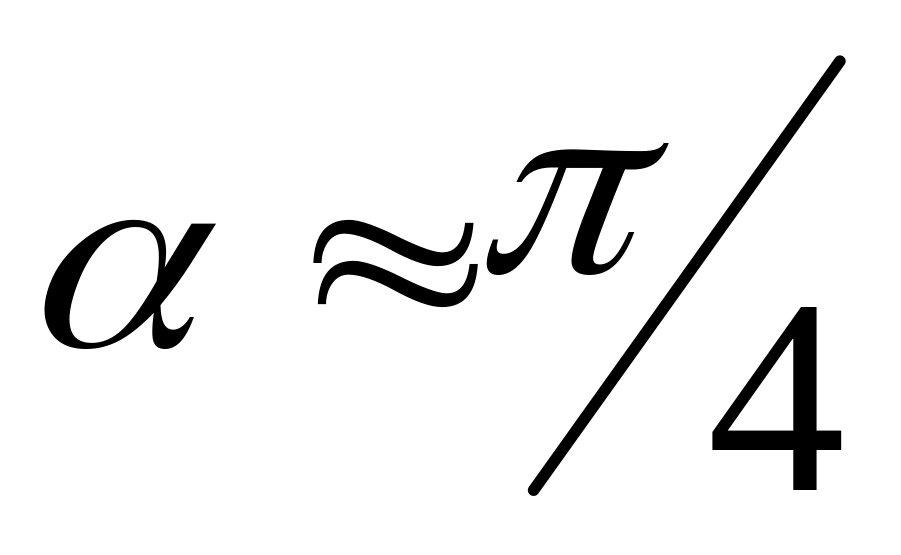
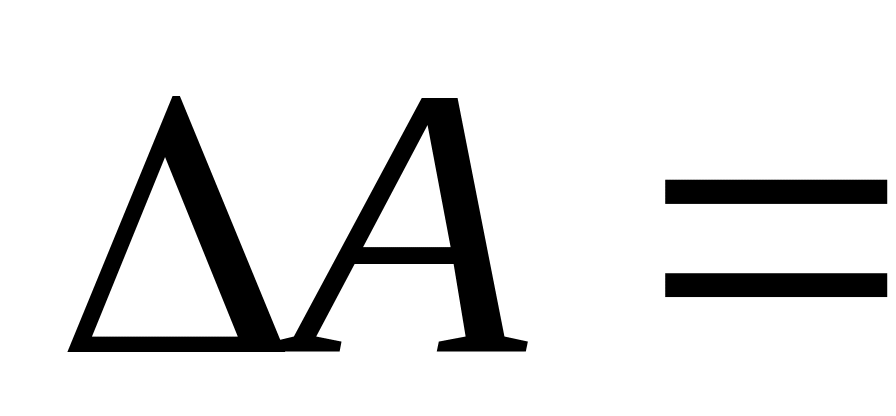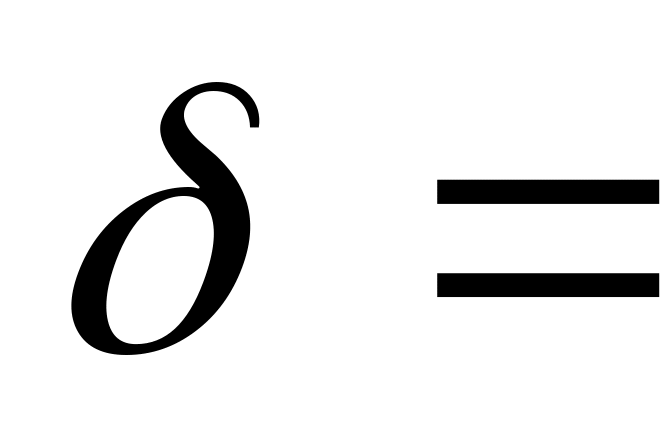		,˚			, с–1
k	1		2	3		4	5	6
Nk
Ak=A0 – kΔA,˚
tk = Nk <T>, с
lnAk
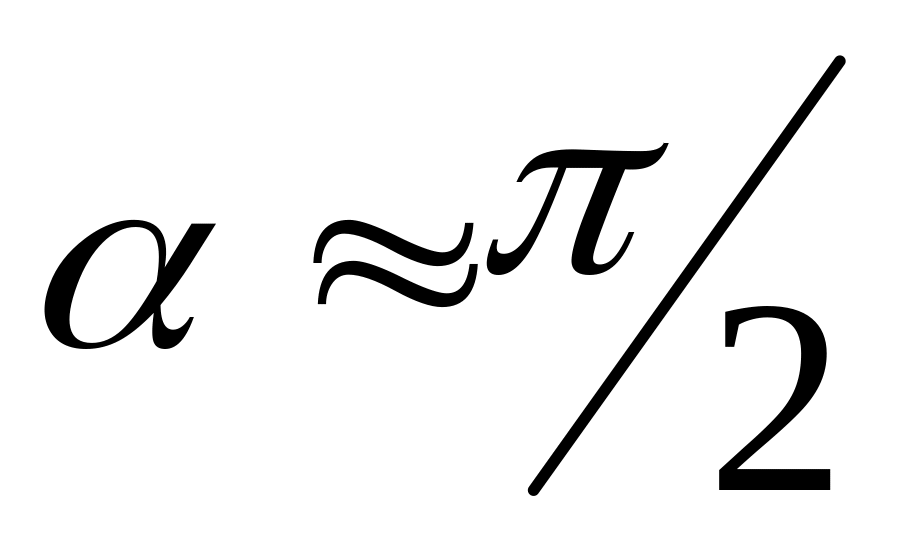
		,˚			, с–1
k	1		2	3		4	5	6
Nk
Ak=A0 – kΔA,˚
tk = Nk <T>, с
lnAk