17. Відкрита транспортна задача, її математична модель. Розвязок відкритої транспортної задачі.

Транспортна задача , для якої сумарні об'єми споживання і постачання співпадають є закритою моделлю, в протилежному випадку - відкритою.

Для відкритої моделі може бути два випадки:

а) сумарні об'єми споживання перевищують сумарні об'єми постачання ;

б) сумарні об'єми постачання перевищують сумарні об'єми споживання .

У випадку, коли сумарні об'єми споживання перевищують сумарні об'єми постачання, вводять фіктивний пункт постачання Вm+1, об'єм поставок якого.

У випадку, коли сумарні об'єми постачання перевищують сумарні об'єми споживання, вводять фіктивного споживача Аn+1

Вартість перевезень одиниці вантажу як до фіктивного споживача, так і вартість одиниці вантажу від фіктивного постачальника приймають рівною нулю.

Після перетворення задача приймає вид закритої моделі і розв'язується звичайним способом.

18. Загальна задача нелінійного програмування. Алгоритм застосування графічного методу розвязку задач нлп

У загальній постановці задачу нелінійного програмуван­ня (НЛП) записують так:

 (1)

(max)z(x1, x2, …, xn), (2)

де F1(x), …, Fn(x),z(x), x=(x1, x2, …,xn) – довільні фун­кції. У конкретних задачах частина обмежень (або всі) можуть бути нерівностями. Крім того, на невідомі можуть на­кладатися умови невід'ємності і т.п.

Однією з основних особливостей задач НЛТ є можливість різними способами задавати цільову функцію. Якщо в лінійному випадку вона була строго монотонною і досягала свого оптимального значення лише у вершині многокутника розв'язку; то тут картина зовсім інша. Наприклад! навіть графік функції, однієї змінної, свідчить про те, що вона вже має багато локальних максимумів.

Друга особливість задач НЛП випливає із порушення властивості опуклості многокутника розв'язків задач ЛП. Легко навести приклади задач, де область розв'язків задачі НЛП буде багатозв'язною.

Алгоритм:

1.Знайти область D допустимих розв’язків задачі,яка визначається системою обмежень,якщо D - порожня множина, то задача розвязку не має.

2.Побудувати гіперповерхню F(x1,x2,…,xn)=h для деякого значення h.

3.Змінюючи значення h, знайти гіперповерхню найвищого(найнижчого) рівня, яка мала хоча б одну спільну точку з областю D. Якщо виявиться, що функція F не обмежена зверху(знизу)на множини D , то відповідна задача на максимум(мінімум) не має розвязку.

4.Якщо розвязок задачі існує, то кожна точка X є D, яка належить гіперповерхні найвищого(найнижчого) рівня,є оптимальною, а відповідне значення функції F(X)– є оптимальним.

Графічний метод є особливо зручним для випадку двох невідомих, оскільки множину обмежень тоді можна зобразити на площині.

19. Задачі дробово-лінійного програмування. Застосування симплексного методу для розв’язування задач дробово-лінійного програмування

Розв’язуючи економічні задачі, часто як критерії оптимальнос­ті беруть рівень рентабельності, продуктивність праці тощо. Ці показники математично виражаються дробово-лінійними функціями. Загальну економіко-математичну модель у цьому разі записують так (розглянемо задачу визначення оптимальних обсягів виробництва продукції): позначимо через   прибуток від реалізації одиниці  -го виду продукції, тоді загальний прибуток можна виразити формулою:  ; якщо   — витрати на виробницт­во одиниці  -го виду продукції, то   — загальні витрати на виробництво. У разі максимізації рівня рентабельності вироб­ництва цільова функція має вигляд: 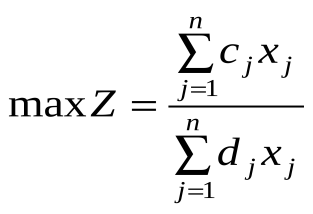 (7.1) за умов виконання обмежень щодо використання ресурсів: ; (7.2) . (7.3) Передбачається, що знаменник цільової функції в області допустимих розв’язків системи обмежень не дорівнює нулю. Очевидно, що задача (7.1)—(7.3) відрізняється від звичайної задачі лінійного програмування лише цільовою функцією, що дає змогу застосовувати для її розв’язування за певного модифікування вже відомі методи розв’язання задач лінійного програмування.

В економіці існує значна кількість процесів, які описуються за допомогою нелінійних моделей. Внаслідок цього постає необхідність у дослідженні та вивченні методів розв’язку оптимізаційних задач, які описуються нелінійними моделями.

Нелінійне програмування – це розділ математичного програмування, в яких цільова функція або хоча б одне з обмежень в системі нелінійними.

Особливість задач нелінійного програмування:

1. В задачах лінійного програмування оптимальні розв’язки завжди знаходиться на межі області допустимих розв’язків. В задачах нелінійного програмування розв’язки можуть знаходитися і всередині області допустимих розв’язків.

2. Для задач нелінійного програмування не існує єдиного універсального методу їх розв’язку. В залежності від виду математичної моделі застосовують різні методи розв’язку.