9. Опорний розвязок. Штучний базис, запис цільової функції та розвязок м-задачі лінійного програмування.
Опорним називають базисний розв’язок, який не містить від’ємних чисел.
Серед опорних розв’язків і міститься оптимальний розв’язок, що максимізує чи мінімізує цільову функцію.
Бувають випадки, коли основне обмеження представлене у вигляді рівняння, проте базисної змінної немає. В таких випадках вводиться штучна змінна ω, призначення якої – формально виконувати роль базисної змінної.
Очевидно, що в кінцевому розв’язку штучна базисна змінна може дорівнювати 0.
Якщо в розв’язку задачі існує хоча б одна базисна змінна, яка б не дорівнювала 0, це означає, що задача розв’язку немає, оскільки система обмежень є несумісною (такою, що немає розв’язків).
Щоб знайти опорний розв’язок та скласти початкову симплексну таблицю, спочатку задачу потрібно записати в канонічному вигляді.
Якщо задача на пошук мінімуму, то цільові функції біля штучної базисної змінної ставиться коефіцієнт +М, якщо задача на максимум, то записується коефіцієнт –М, де М – дуже велике число.
Оскільки задача на мінімум, то не повинно бути додатніх оцінок. Серед існуючих додатніх оцінок вибираємо найбільшу по модулю.
В останній симплексній таблиці існує змінна, яка не є базисною, проте її оцінка рівна 0. Якщо в останній симплексній таблиці змінна, що не є базисною, має нульову оцінку, це означає, що задача має не один розв’язок.
Для того, щоб знайти інший розв’язок, необхідно в базис ввести ту змінну, яка має нульову оцінку.
Між оптимальними розв’язками вихідної задачі і М-задачі існує наступний зв’язок: якщо в оптимальному розв’язку М-задачі усі штучні змінні ωі рівні нулю, то значення усіх інших координат розв’язку х̄ дадуть оптимальний розв’язок вихідної задачі. Якщо хоча б одна із змінних ωі не дорівнює нулю, то вихідна задача немає розв’язку.
Звертати увагу слід лише на ті числа, що стоять над нулями нижнього рядка.
10. Основна та двоїста задачі як пара взаємоспряжених задач. Правила побудови двоїстої задачі. Знаходження розв’язків однієї задачі по розвязках іншої.
До будь-якої задачі лінійного програмування можна поставити у відповідність двоїсту задачу. Задача, до якої поставлено двоїсту, називається пряма задача. Пряма і поставлена до неї двоїста задачі називаються взаємно спряженими задачами. Особливістю взаємоспряжених задач є те, що коли пряма задача має розв’язок, то і двоїста має розв’язок, при чому їхні розв’язки взаємопов’язані певним чином. Крім того, якщо пряма задача має деякий економічний зміст, то економічний зміст має і двоїста задача.
Для побудови
двоїстої задачі необхідно звести
пряму задачу до стандартного виду.
Вважають, що задача лінійного програмування
подана у стандартному вигляді, якщо для
відшукання максимального значення
цільової функції всі нерівності її
системи обмежень приведені до виду «
»,
а для задачі на відшукання мінімального
значення — до виду «
».
Якщо пряма задача лінійного програмування подана в стандартному вигляді, то двоїста задача утворюється за такими правилами: 1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.
2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень двоїстої задачі дорівнює кількості невідомих прямої задачі.
3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі — на визначення найменшого значення (min), і навпаки.
4. Коефіцієнтами при змінних у цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.
5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних у цільовій функції прямої задачі.
6. Матриця
,
що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі обмежень двоїстої задачі
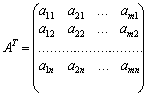
утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків — рядками.