
- •Информационно-технологический факультет Кафедра информационных технологий и управляющих систем
- •Контрольные вопросы и задачи к лекции 1
- •Лекция 2. Виды воздействий на сау
- •2.1. Классификация видов воздействий на сау Виды воздействий на сау описываются переходной, весовой, передаточной функциями.
- •2.2. Импульсные функции
- •Лекция 3. Преобразования Фурье и Лапласа
- •3.1. Преобразование Фурье
- •Лекция 4. Преобразование Лапласа
- •Контрольные вопросы и задачи к лекции 4
- •Лекция 5. Понятие линейного динамического звена
- •5.1. Уравнение линейного динамического звена
- •5.2. Передаточная функция линейного динамического звена
- •5.3. Структурная схема динамического звена
- •Контрольные вопросы и задачи к лекции 5
- •Лекция 6. Временные характеристики динамического звена
- •Контрольные вопросы и задачи к лекции 6
- •Лекция 7. Частотные характеристики динамического звена
- •Контрольные вопросы и задачи к лекции 7
- •Лекция 8. Элементарные (типовые) динамические звенья
- •Контрольные вопросы и задачи к лекции 8
- •Лекция 9. Временные и частотные характеристики звеньев
- •Контрольные вопросы и задачи
- •Лекция 7. Правила эквивалентных преобразований структурных схем систем автоматического управления
- •Принцип суперпозиции (наложения)
- •Контрольные вопросы и задачи
- •Лекция 8 Ориентированные графы систем автоматического управления
- •Использование формулы Мейсона для преобразования структурных схем и ориентированных графов
- •Контрольные вопросы и задачи
- •Лекция 9 Логарифмические частотные характеристики динамических звеньев
- •Логарифмические частотные характеристики элементарных динамических звеньев
- •Контрольные вопросы и задачи
- •Лекция 10 Логарифмические частотные характеристики систем автоматического управления
- •Контрольные вопросы и задачи
- •Лекция 11 Временные и частотные характеристики колебательного звена
- •Контрольные вопросы и задачи
- •Семестр 2 Лекция 12 Понятие многомерной системы
- •Контрольные вопросы и задачи
- •Лекция 13 Структурные матричные схемы и передаточные матрицы
- •Контрольные вопросы и задачи
- •Лекция 14 Математические модели в пространстве состояний
- •Контрольные вопросы и задачи
- •Лекция 15 Взаимосвязь видов математических моделей многомерных систем
- •Контрольные вопросы и задачи
- •Лекция 16 Методы оценки качества систем управления
- •Оценка качества переходного процесса при воздействии ступенчатой функции
- •Контрольные вопросы и задачи
- •Лекция 17 Оценка качества при гармонических воздействиях
- •Лекция 9. Интегральные оценки качества сау
- •Контрольные вопросы и задачи
- •Лекция 18 Вычисление линейных интегральных оценок
- •Квадратичная интегральная оценка
- •Контрольные вопросы и задачи
- •Лекция 19 Квадратичная интегральная оценка с учетом производной
- •Вычисление квадратичных интегральных оценок
- •Контрольные вопросы и задачи
- •Лекция 20 Корневые критерии качества переходных процессов
- •Контрольные вопросы и задачи
- •Лекция 21 Определения и задачи идентификации математических моделей
- •Контрольные вопросы и задачи
Оценка качества переходного процесса при воздействии ступенчатой функции
Прямые оценки качества определяют по графику переходной характеристики системы управления , то есть при воздействии на систему единичной ступенчатой функции –
![]()
и при нулевых
начальных условиях, или по кривой
переходного процесса регулируемой
переменной
![]() при
воздействии на вход ступенчатой функции
с амплитудой, соответствующей номинальному
или иному определенному значению
регулируемой переменной.
при
воздействии на вход ступенчатой функции
с амплитудой, соответствующей номинальному
или иному определенному значению
регулируемой переменной.
Рассмотрим систему управления с единичной отрицательной обратной связью, структурная схема которой показана на рис. 2.
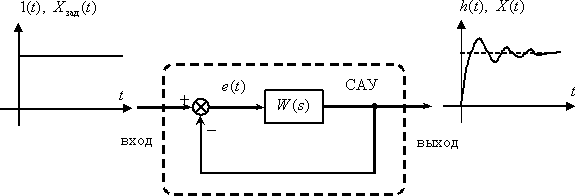
Рис. 3
На вход системы поступает ступенчатый сигнал, на выходе можно наблюдать реакцию системы, кроме того, в качестве переходного процесса может рассматриваться изменение ошибки регулирования –
![]() .
.
Примерные графики изменения сигнала на выходе и ошибки регулирования показаны соответственно на рис. 4 и 5.
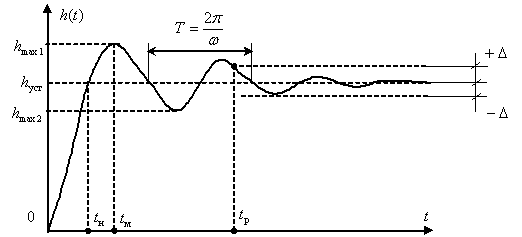
Рис. 4
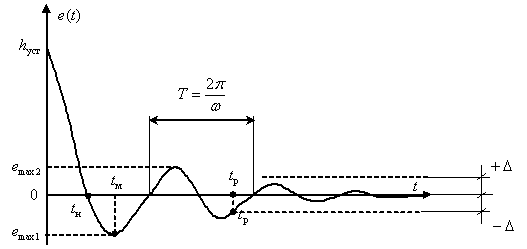
Рис. 5
Рассмотрим прямые оценки качества переходных процессов, показанные на рис. 4 и 5:
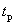 –
минимальное время,
по истечении которого регулируемая
величина будет оставаться близкой к
установившемуся значению с заданной
точностью –
–
минимальное время,
по истечении которого регулируемая
величина будет оставаться близкой к
установившемуся значению с заданной
точностью –
![]() .
.
![]() предварительно
задается в процентах от установившегося
значения
предварительно
задается в процентах от установившегося
значения
![]() ,
где нет определенных требований –
принимают
,
где нет определенных требований –
принимают
![]() .
.
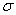 –
перегулирование
– максимальное отклонение от
установившегося значения, выраженное
в относительных единицах или процентах
–
–
перегулирование
– максимальное отклонение от
установившегося значения, выраженное
в относительных единицах или процентах
–
![]() или
или
![]() .
.
Обычно требования
по перегулированию составляют
![]() ,
иногда к качеству процессов может быть
предъявлено требование
,
иногда к качеству процессов может быть
предъявлено требование
![]() ,
на пример в системах позиционирования
манипуляторов промышленных роботов.
,
на пример в системах позиционирования
манипуляторов промышленных роботов.
– частота колебаний –
![]() ,
,
где – период колебаний для колебательных процессов.
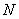 –
это число полных
колебаний, которое имеет
или
–
это число полных
колебаний, которое имеет
или
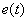 за
время регулирования
,
обычные требования по числу колебаний
за
время регулирования
,
обычные требования по числу колебаний
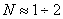 ,
в некоторых системах накладывают
ограничение на колебательность
,
в некоторых системах накладывают
ограничение на колебательность
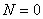 ,
на пример, в системах с существенным
люфтом в механических передачах.
,
на пример, в системах с существенным
люфтом в механических передачах.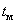 –
время достижения
первого максимума.
–
время достижения
первого максимума.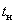 –
время нарастания
переходного процесса, время от начала
переходного процесса до момента первого
пересечения графиком линии установившегося
значения.
–
время нарастания
переходного процесса, время от начала
переходного процесса до момента первого
пересечения графиком линии установившегося
значения.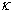 –
декремент затухания,
равный отношению модулей двух смежных
перерегулирований –
–
декремент затухания,
равный отношению модулей двух смежных
перерегулирований –
 .
.
Перечисленные выше показатели могут быть дополнены и другими, если этого требуют специфические технические задания на разработку или исследование систем управления.
Устойчивые переходные процессы, возникающие при ступенчатом воздействии, принято делить на три группы:
Монотонные процессы. Такие процессы, где первая производная выходной величины по времени не меняет знак.
Апериодические процессы. Здесь производная меняет знак не более одного раза.
Колебательные процессы. Производная меняет свой знак периодически
На рис. 6 показан примерный вид колебательного, апериодического и монотонного процессов.
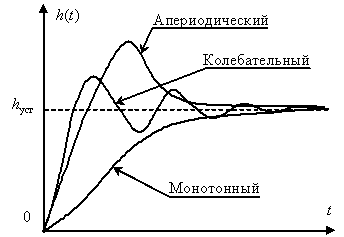
Рис. 6
Требования к качеству переходного процесса могут быть представлены графически. Они сводятся к требованию, чтобы отклонение регулируемой величины при ступенчатом воздействии не выходило за границы некоторой области, изображенной на диаграмме качества процесса. Простейшая диаграмма показана на рис. 7.

Рис. 7
Уточненная
диаграмма, в которой накладываются
ограничения на скорость нарастания
сигнала, показана на рис. 8. На уточненной
диаграмме
![]() обозначает
время запаздывания, равное отрезку
времени, заключенному между моментами
приложения скачкообразного сигнала
(
)
и моментом времени, при котором выходная
величина достигает половины установившегося
значения.
обозначает
время запаздывания, равное отрезку
времени, заключенному между моментами
приложения скачкообразного сигнала
(
)
и моментом времени, при котором выходная
величина достигает половины установившегося
значения.
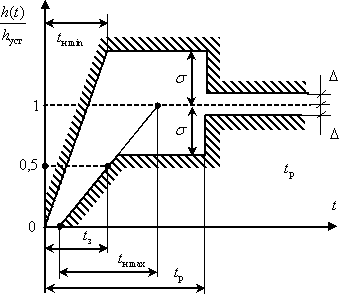
Рис. 8
