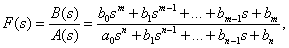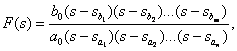КОРОЛЕВСКИЙ ИНСТИТУТ

УПРАВЛЕНИЯ, ЭКОНОМИКИ И СОЦИОЛОГИИ

Информационно-технологический факультет Кафедра информационных технологий и управляющих систем

Дисциплина: МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

КОНСПЕКТ ЛЕКЦИЙ

Королев - 2012

Введение

Теория автоматического управления (ТАУ) — это дисциплина, изучающая процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию.

Семестр 1

Лекция 1. Передаточные функции систем автоматического управления

Для представления передаточных функций, а также решения задач синтеза и анализа САУ широко используют дробно-рациональные функции комплексного переменного в различных формах.

Дробно-рациональная функция некоторого действительного или комплексного переменного имеет следующий вид:

(1)

где - полиномы числителя и знаменателя, - действительные числа, - порядок числителя, - порядок знаменателя (всей дробно-рациональной функции), - для функций, используемых в ТАУ.

Полиномы дробно-рациональной функции могут быть представлены в виде произведения биномов (разложение многочлена на сомножители), тогда функция может быть представлена в форме Боде

(2)

где - корни уравнения , - корни характеристического уравнения .

Корни уравнения называют нулями дробно-рациональной функции , так как

.

Корни характеристического уравнения называют полюсами дробно-рациональной функции, так как

.

Полюсы и нули могут быть действительными и комплексно-сопряженными числами. Таким образом, задача представления функции в форме Боде сводится к поиску корней уравнений, образованных полиномами числителя и знаменателя.

Их принято располагать на плоскости комплексной переменной , обозначая расположение полюсов крестиками, а нулей кружками. Для лучшего освоения этого материала необходимо освежить в памяти сведения из высшей математики по операциям с комплексными числами. Нули, а особенно полюсы дробно-рациональных функций изображают на плоскости комплексного переменного . На рис. 1 показано расположение полюсов и нулей некоторой дробно-рациональной функции.

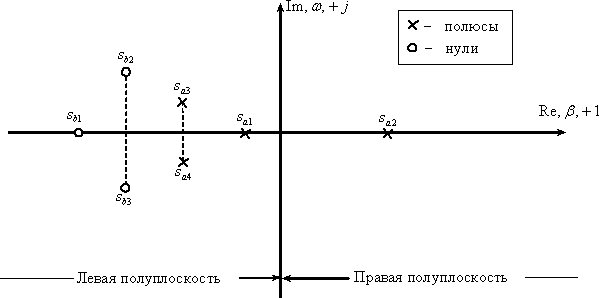
Рис. 1

Мнимая ось делит плоскость на правую и левую полуплоскости. Нули и полюсы, расположенные в правой полуплоскости, называют правыми, в левой полуплоскости – левыми. Комплексные полюсы и нули всегда располагаются парами симметрично относительно действительной оси; такие пары корней называют комплексно сопряженными корнями. Если среди нулей и полюсов встречаются два или несколько одинаковых, их называют кратными в отличие от остальных, которых называют простыми. Кратность определяется числом одинаковых нулей или полюсов ( – 2). Рассмотрим пример получения формы Боде.

Пример

Представьте дробно-рациональную функцию

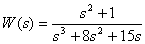
в форме Боде и покажите расположение полюсов и нулей дробно-рациональной функции на комплексной плоскости.

Решение

Найдем корни уравнения

.

Получаем два комплексно-сопряженных корня (нуля)

, .

Найдем полюсы

.

Получаем три полюса

.

Покажем расположение нулей и полюсов на комплексной плоскости (см. рис. 2).

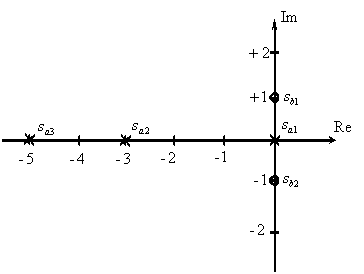
Рис. 2

Дробно-рациональную функцию (1) часто представляют в виде суммы простейших дробей (форма Хэвисайда)

(3)

где – корни характеристического уравнения , – коэффициенты разложения, которые находят по следующей функции:

(4)

Такое представление дробно-рациональной функции возможно, если полюсы – простые, а .

Функция, которая имеет один нулевой полюс, может быть представлена в следующем виде:

В этом случае вместо формул (3), (4) применяют выражение

(5)

где – ненулевые полюсы , корни уравнения ,

(6)

Следовательно, представление дробно-рациональной функции в форме Хэвисайда сводится к нахождению полюсов дробно-рациональной функции и рациональному использованию формул разложения. Рассмотрим ряд примеров получения формы Хэвисайда.

Пример

Представьте дробно-рациональную функцию

в форме Хэвисайда, используя формулы разложения (3), (4).

Решение

Уравнение полинома числителя имеет вид

.

Характеристическое уравнение имеет вид

.

Найдем корни характеристического уравнения

, .

Определим производную от полинома знаменателя

.

Определим коэффициенты разложения соответствующие по номеру полюсам

, .

Тогда форма Хэвисайда имеет вид

.

Пример

Представьте дробно-рациональную функцию

в форме Хэвисайда, используя формулы разложения (5), (6).

Решение

Представим в виде

Тогда

,

.

Ненулевые полюсы имеют вид

, .

Производная от

.

Определим коэффициенты разложения

, , .

Тогда форма Хэвисайда имеет вид

.