Запись десятичной дроби в виде обыкновенной и наоборот

С выражением десятичной дроби в виде обыкновенной учащие­ся уже сталкивались неоднократно. Во-первых, образование деся­тичной дроби рассматривалось как частный случай обыкновенной дроби, у которой знаменатель — единица с нулями, во-вторых, десятичную дробь в виде обыкновенной учащиеся выражали при знакомстве с действиями над десятичными дробями. Запись деся­тичной дроби в виде обыкновенной сводится к записи десятичной

дроби со знаменателем, например: 0,3=3/10; 0,07=7/100

1,873=1 873/1000.

Обратное упражнение, т. е. запись обыкновенной дроби в виде десятичной, выполняется так:

У обыкновенной дроби 1/5 знаменатель дроби 5, у десятичной

же дроби знаменатель должен выражаться единицей с нулями, т. е. 10, 100, 1000 и т. д. Подбираем такое число, при умножении на которое числа 5 получалось бы 10, 100, 1000, т. е. знаменатель дроби выразился бы единицей с нулями. Если 5▪ 2, то получится 10. Чтобы дробь не изменилась, надо и числитель умножить на 2.

Следовательно, 1/5 = 2/10=0,2. Запишем дробь 3/4 в виде деся-

336

тичной. Для этого нужно, чтобы знаменатель этой дроби стал равен 10, 100 или 1000. В десятых долях эту дробь выразить нельзя, так как 10 не делится на 4 нацело. Посмотрим, нельзя ли вы­разить эту дробь в сотых долях: 100:4=25. Значит, и числитель, и знаменатель дроби ¾ надо умножить на 25 (дополнительный множитель 25). Следовательно, ¾=75/100=0,75. Выразим дробь 5/8 в десятичных долях. Знаменатель 10 не подходит, так как 10 не делится на 8 нацело, знаменатель 100 тоже не подходит по той же причине, попробуем взять знаменатель 1000:8=125 (до­полнительный множитель 125). Следовательно. 5/8= 625/1000=0,625.

Но не всегда этим способом можно (при замене обыкновенной дроби десятичной) выразить знаменатель обыкновенной дроби 1 с несколькими нулями. Возьмем, например, дробь 1/3. Попробуем взять знаменатель 10. Он не подходит, так как нельзя в данном случае получить дополнительный множитель: 10 не делится наце­ло на 3. То же получим, если возьмем знаменатели 100, 1000. Следовательно, дробь 1/3 нельзя этим способом выразить десятич­ной дробью.

Существует второй способ замены обыкновенной дроби деся­тичной. Всякую обыкновенную дробь можно рассматривать как частное от деления числителя на ее знаменатель. Возьмем дробь 3/4. Ее можно рассматривать как частное от деления 3 на 4. Выпол­ним деление:

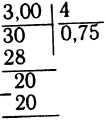
Рассуждение: «3 на 4 не делится нацело. В част­ном пишем нуль целых и ставим после нуля запя­тую. Раздробляем 3 в десятые доли. 30 десятых делим на 4. В частном пишем 7 десятых. В остатке 2 десятых. Раздробим 2 десятых в сотые доли. Полу­чим 20 сотых. Делим на 4. В частном 5 сотых.

Итого в частном 0,75. Следовательно, 3/4=0,75».

Проверка. Нужно частное умножить на делитель. В произве­дении должно получиться число, равное делимому:

0,75▪4=3.

337

1,000	3
10 - 9	0,3333...
10 - 9
10 9
- 10 9

После рассмотрения еще нескольких примеров учащиеся долж­ны сами сделать вывод о том, как обыкновенную дробь заменить десятичной.

«Вернемся к дроби . Мы видели, что

что дробь нельзя заменить десятичной первым

способом. Попробуем заменить ее десятичной вторым способом, т. е. делением числителя на знаменатель. Если будем продолжать делить дальше, то увидим, что всегда в остатке будет единица, а в частном 3. Деление можно про­должить бесконечно. Но обычно его прерыва­ют, делят до первого, второго или третьего знака после запятой, например: 1:3=0,333...». В данном случае деление закончили на тысячных долях. Точки показывают, что деление можно продолжить и дальше. 0,333... — приближенное, неточное значение дроби . Можно предложить учащимся обратить в десятичные еще ряд обыкновенных дробей: , , , , и т.д.

Получаются приближенные десятичные дроби.

После рассмотрения замены различных обыкновенных дробей десятичными учащиеся убеждаются, что одни обыкновенные дроби можно точно выразить десятичными — в этом случае полу­чаются конечные десятичные дроби ( = 0,2), другие же можно заменить только бесконечными десятичными дробями

( = 0,333...).»

Совместные действия с обыкновенными и десятичными дробями

После изучения обыкновенных и десятичных дробей программой предусмотрены совместные действия над дробями. Перед изучением этой темы следует повторить отдельно все действия над обыкновен­ными и десятичными дробями, устно и письменно закрепить замену обыкновенной дроби десятичной и наоборот. Все эти виды упражне­ний должны быть хорошо отработаны, иначе учащиеся при выполне­нии совместных действий с дробями столкнутся с непреодолимыми трудностями, что вызовет у школьников с нарушением интеллекта чувство беспомощности, негативное отношение к работе.

338

При выполнении совместных действий с десятичными и обыкно­венными дробями в школе VIII вида, как показывает опыт, целесооб­разнее либо все обыкновенные дроби заменять десятичными и вы­полнять действия только над десятичными дробями, либо наоборот.

Сначала решаются задачи и примеры с двумя компонентами. Учитель, объясняя, как выполнить действие, должен обратить внимание учащихся на целесообразность замены дробей десятич­ными или обыкновенными. Например, в примере 0.45+ целесообразно дробь заменить десятичной, так как это сделает вычис­ления более простыми. Если же 0,45 заменить обыкновенной дро­бью, то вычисления будут более громоздкими.

В этом учащихся следует убедить, предложив выполнить дейст­вия сначала в десятичных, а затем в обыкновенных дробях:

1,45+ = ? 1,45 = 1 = 1

= 0,5 1 + = = = 1

Сначала учитель подсказывает учащимся, с какими дробями целесообразнее выполнять действия.

По мере накопления опыта учащиеся сами должны выбирать наиболее удобные пути решения в каждом конкретном случае.