
- •Інтерпретація гіперболічної геометрії в евклідовому просторі
- •§1. Псевдосфера
- •Про моделі площини Лобачевського
- •Кривизна псевдосфери
- •Відображення псевдосфери на евклідову площину
- •§2. Карти гіперболічної площини в евклідовому просторі. Карта Пуанкаре
- •2.1 Гіперболічні рухи півплощини площини
- •2.2 Гіперболічні прямі півплощини
- •2. 3 Карта Пуанкаре.
- •§3. Карти гіперболічної площини в евклідовому просторі. Карта Бельтрамі
- •3.1 Перехід від карти Пуанкаре до карти Бельтрамі
- •3.2 Вимірювання відрізків на карті Бельтрамі
- •3.3 Формули гіперболічної тригонометрії. Прямокутний трикутник.
- •3.4 Формули гіперболічної тригонометрії. Косокутний трикутник.
- •Розділ іі аналітична геометрія на площині лобачевського
- •§1. Координати точки. Різні випадки рівняння прямих
- •1.1 Полярні, веєрштрасові та однорідні координати точки
- •1.2 Перетворення координат.
- •1.3 Загальний випадок перетворення координат.
- •1.4 Пряма
- •Інваріанти перетворення координат.
- •Про перетин двох прямих
- •Рівняння прямої, що проходить через дві дані точки
- •Координати середини відрізка
- •9 Про уявні точки та прямі
- •§2. Криві другого порядку
- •1.1 Криві другого порядку і другого класу
- •Класифікація кривих другого порядку
- •1.3 Рівняння граничної лінії
- •Розділ ііі початки диференціальної геометрії гіперболічної площини
- •§1. Вейєрштрасові, полярні та прямокутні координати
- •1.1 Диференціал дуги. Вейєрштрасові координати
- •1.2 Диференціал дуги. Полярні координати
- •1.3 Прямокутні координати. Диференціал дуги в прямокутних координатах
- •1.4 Довжина кола. Довжина дуги еквідистанти і граничної лінії
- •§2. Деякі плоскі криві в геометрії Лобачевського
- •2.1 Дотична і нормаль до плоскої кривої
- •2.2 Кривина плоскої кривої
- •2.3 Орициклоїда
- •2.4 Трактриса та її еволюта
Інваріанти перетворення координат.
Нехай в результаті перетворення координат:
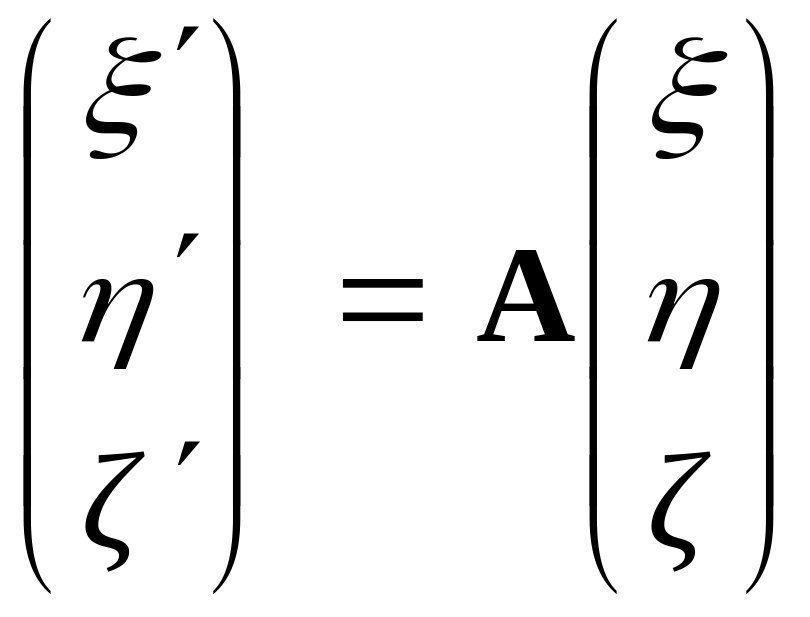 (38)
(38)
Тоді
рівняння
![]() якоїсь прямої набирає вигляду:
якоїсь прямої набирає вигляду:
![]() .
.
Встановимо залежність між величинами u, v, w і u', v', w'. Насамперед будемо мати:
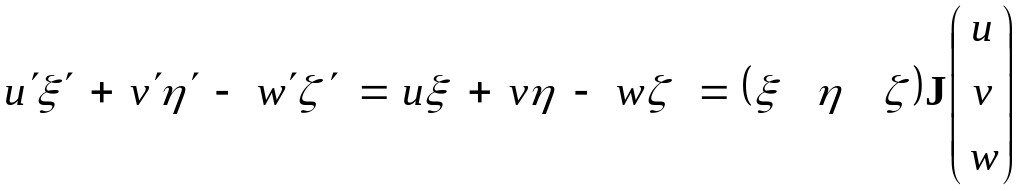 .
(39)
.
(39)
Далі аналогічно до формул (16) і (18):
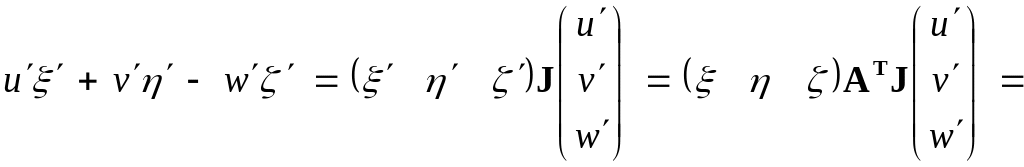
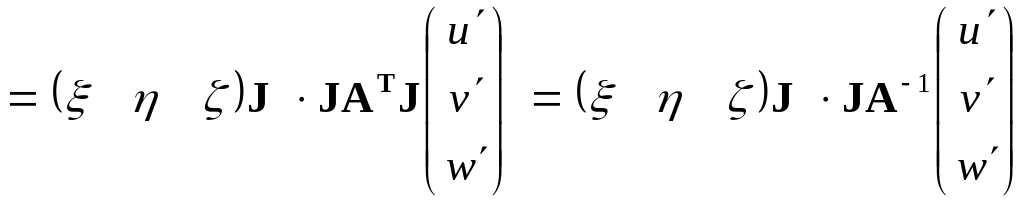 .
(40)
.
(40)
Якщо порівняти рівності (39) і (40), то можемо побачити, що
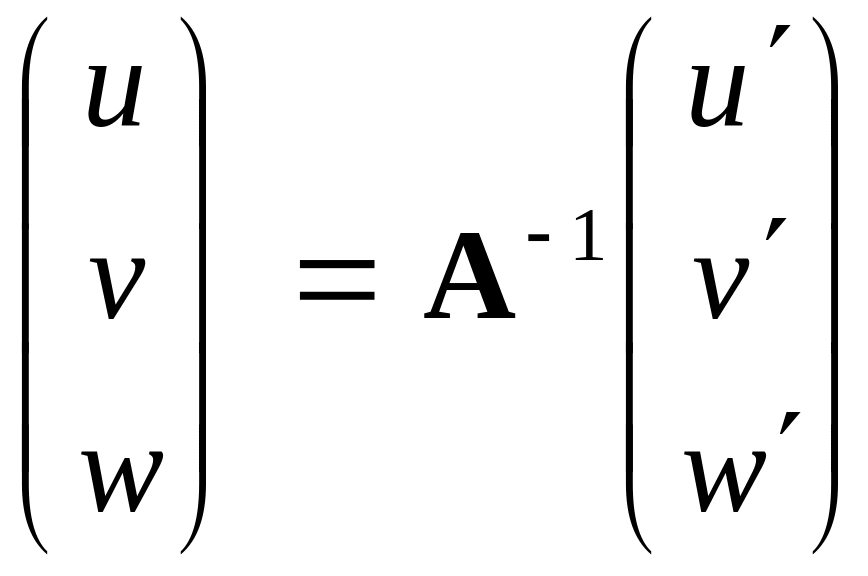 або
або
 .
.
Отже, при переході до нової системи координат, матриці перетворення вейєрштрасових (а також однорідних) координат точки і координат прямої залишаються тими ж, а це означає що величини ξ, η, ζ (або однорідні координати x, y, z) і u, v, w змінюються когредієнтно.
Це міркування застосуємо до окремих випадків:
1. Нехай дано точки P1 і P2 з їх вейєрштрасовими координатами ξ1, η1, ζ1 і ξ2, η2, ζ2. Внаслідок когредієнтності цих змінних величина
![]() (41)
(41)
є
інваріант перетворення координат.
З’ясуємо геометричний зміст величини
![]() .
Приймемо точку P1
за новий початок координат O',
а пряму P1P2
за вісь O'X',
що має напрям від P1
до P2
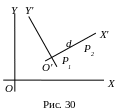
(рис. 30). Нехай P1P2
=
d.
.
Приймемо точку P1
за новий початок координат O',
а пряму P1P2
за вісь O'X',
що має напрям від P1
до P2
(рис. 30). Нехай P1P2
=
d.
Визначимо нові координати точок P1, P2:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Отже,
![]() .
(42)
.
(42)
Порівнюючи (41) і (42), дістаємо формулу:
![]() ,
(43)
,
(43)
яка служить для визначення відстані між двома точками.
2.
Нехай дано точку P
її вейєрштрасовими координатами ξ,
η,
ζ
і пряму l
її
нормальним рівнянням
![]() .
Внаслідок когредієнтності змінних ξ,
η,
ζ
і u,
v,
w
величина
.
Внаслідок когредієнтності змінних ξ,
η,
ζ
і u,
v,
w
величина
![]() (44)
(44)
є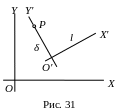 інваріант перетворення координат. Для
з’ясування її геометричного змісту
візьмемо l
за вісь O'X',
а пряму, яка проходить через P
і перпендикулярна до l,
за вісь O'Y'
(рис. 31). Позначимо відстань від точки P
до прямої l
через δ (
інваріант перетворення координат. Для
з’ясування її геометричного змісту
візьмемо l
за вісь O'X',
а пряму, яка проходить через P
і перпендикулярна до l,
за вісь O'Y'
(рис. 31). Позначимо відстань від точки P
до прямої l
через δ (![]() ).
Визначимо нові координати точки P:
).
Визначимо нові координати точки P:
![]() ,
,
![]() ,
,
![]()
і нові координати прямої l:
![]() ,
,
![]() ,
,
![]() .
.
Звідси
![]() .
(45)
.
(45)
Із (44) та (45) дістаємо формулу:
![]() ,
(46)
,
(46)
Яка служить для визначення відстані від точки до прямої.
3.
Нехай прямі l1
і
l2
задані відповідно їх нормальними
рівняннями:
![]() ,
,
![]() .
.
Як і вище, можна зробити висновок, що величина
![]() (47)
(47)
є інваріант перетворення координат.
 Розглянемо такі
випадки:
Розглянемо такі
випадки:
Прямі l1 і l2 перетинаються у власній точці й утворюють кут ϴ. Приймемо точку перетину цих прямих за новий початок координат O' і пряму l1 за вісь O'X' (рис. 32).
Визначаємо нові координати даних прямих [порівнюючи (31)]:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Звідси
![]() .
(48)
.
(48)
Із (47) і (48) дістаємо формулу:
![]() ,
(49)
,
(49)
яка служить для визначення кута між двома прямими, що перетинаються. Із (49) легко знаходимо умову перпендикулярності двох прямих:
![]() .
(50)
.
(50)
Нехай прямі l1 і l2 — паралельні. Приймемо l1 за вісь за вісь O'X' і визначимо нові координати даних прямих [порівнюючи (36)]:
, , .
![]() ,
,
![]() ,
,
![]() .
.
Звідси
![]() (51)
(51)
Із (47) і (51) робимо висновок, що для паралельних прямих
![]() (52)
(52)
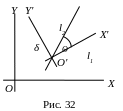
с) Прямі l1 і l2 — розбіжні. Позначимо найкоротшу віддаль між цими прямими через Δ і позначимо їх спільний перпендикуляр за вісь O'X', а пряму l1 за вісь O'Y' (рис. 33).
в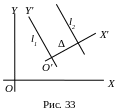 изначимо
нові координати прямих l1
і
l2
[порівнюючи
(32)]:
изначимо
нові координати прямих l1
і
l2
[порівнюючи
(32)]:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Звідси
![]() (53)
(53)
Порівнюючи (47) і (53), дістаємо формулу:
![]() ,
(54)
,
(54)
яка служить для визначення найкоротшої відстані між двома розбіжними прямими.
Зіставляючи формули (49), (52) і (54) можна прийти до висновку, що:
прямі,
задані нормальними рівняннями
![]() і
і
![]() ,
перетинаються у власній точці, будуть
паралельні чи розбіжні, залежно від
того, чи величина
,
перетинаються у власній точці, будуть
паралельні чи розбіжні, залежно від
того, чи величина
![]()
менша, рівна чи більша одиниці.
