1.2 Перетворення координат.

Нехай дано вейєрштрасові координати ξ, η, ζ (або однорідні координати x, y, z) якоїсь точки P гіперболічної площини відносно системи осей OX, OY (старої системи) і треба визначити вейєрштрасові координати ξ', η', ζ' (відповідно однорідні координати x', y,' z') тієї ж точки відносно системи осей O'X', O'Y' (нової системи) причому обидві системи осей конгруентні: будемо вважати, що вісь OY (аналогічно вісь O'Y' ) утворюється з осі OX (відповідно осі O'X'), якщо останню повернути на кут проти годинникової стрілки. Полярні координати точки P будемо позначати через ρ, φ, якщо за полярну вісь взято промінь OX і через ρ', φ', якщо за полярну вісь взято промінь O'X'.

Р озглянемо три випадки перетворення координат:

1). Поворот осей. Нехай стара і нова системи осей мають спільний початок координат O (рис. 26) і нехай

.

В такому випадку

;

тому

, , .

Звідси, беручи до уваги формули (1), дістанемо:

,

,

_.

_{Останні рівності можна записати так:}

_{, (5)}

де

.

Аналогічно дістаємо:

_{. (6)}

2. Трансляція осі. Нехай нова система осей утворюється із старої таким переміщенням, при якому вісь OX ковзає сама по собі (рис. 27). Це перетворення називатимемо трансляцією осі OX. Аналогічно можна розглядати трансляцію осі OY. Позначимо ОО' через δ . Зауважимо, що η' = η.

Далі за теоремою косинусів для косокутного трикутника ОО'P дістаємо:

або

.

Скористаємося тепер тотожністю:

,

З неї отримаємо:

,

Звідси

. (7)

Якщо порівняти старі і нові координати точки О:

, , ,

, , ,

то побачимо, що в правій частині рівності (7) перед дужками потрібно взяти знак +. Отже, в кінцевому випадку в разі трансляції осі OX формули перетворення координат матимуть вигляд:

,

, (8)

або

, (9)

де

Аналогічно:

. (10)

1.3 Загальний випадок перетворення координат.

В загальному випадку перехід до нової системи осей можна здійснити за допомогою трьох послідовних перетворень (рис. 28):

1) Повернувши осі OX, OY навколо початку координат O на кут α так, щоб вісь OX пройшла через новий початок координат O', приходимо до системи осей OX'', OY''.

2) Повернувши вісь OX'' саму по собі на відстань ОО' = δ, приходимо до системи осей O'X''', O'Y'''.

3) Повертаємо осі O'X''', O'Y''' на кут β так, щоб вісь O'X''' сумістилася з віссю O'X'.

Формули цих перетворень мають вигляд:

, , .

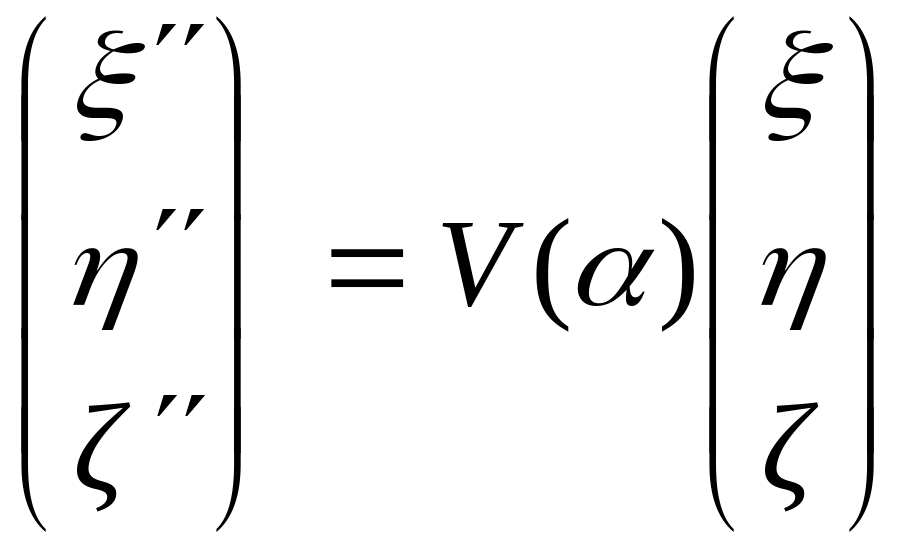Звідси

,

, (11)

,

або

, (12)

де

.

Аналогічно дістаємо:

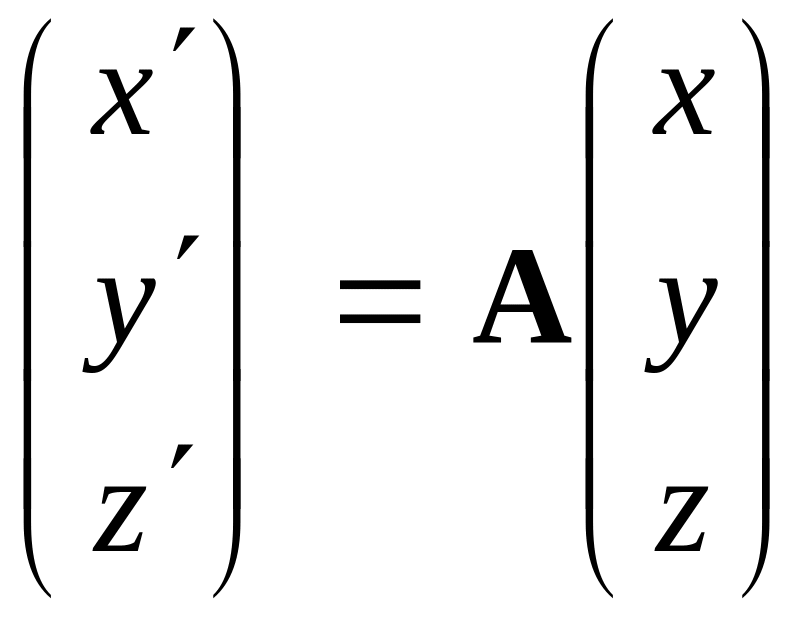_{. (13).}

Визначники кожної з матриць V(α), V(β), T(δ) дорівнюють одиниці, а тому визначник матриці А теж дорівнюватиме одиниці. До того ж квадратичні форми

і

будуть автоморфними відносно перетворень (5), (6), (9), (10), (12), (13), тобто:

,

. (14)

Позначимо через А^-1 матрицю, обернену до квадратної матриці А, і через В^т – транспоновану прямокутну матрицю В, нехай також

, .

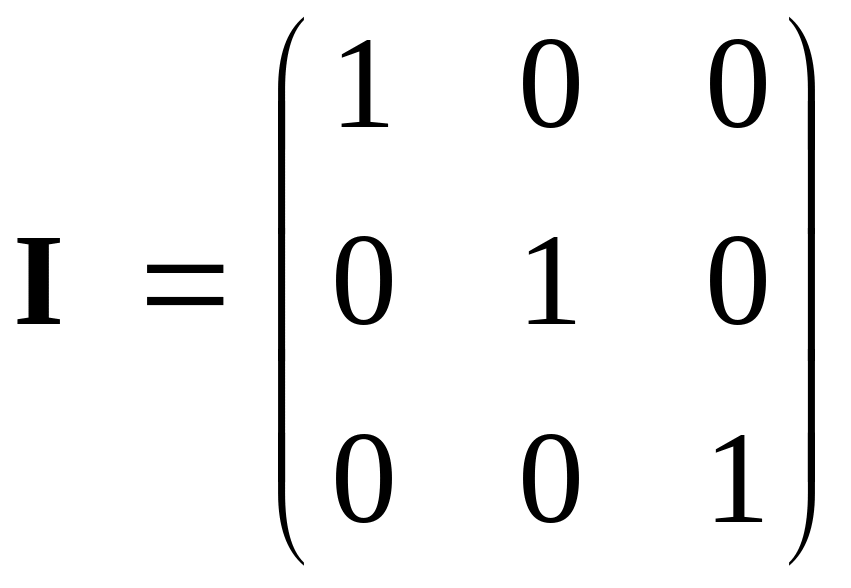Відмітимо такі співвідношення: , , , .

Запишемо першу з рівностей (14) так:

. (15)

Транспонуючи обидві частини рівності (12), отримаємо:

(16)

Із (12) та (16) виводимо, що

. (17)

Порівнюючи (15) і (17), дістаємо:

(18)

звідси

або

.

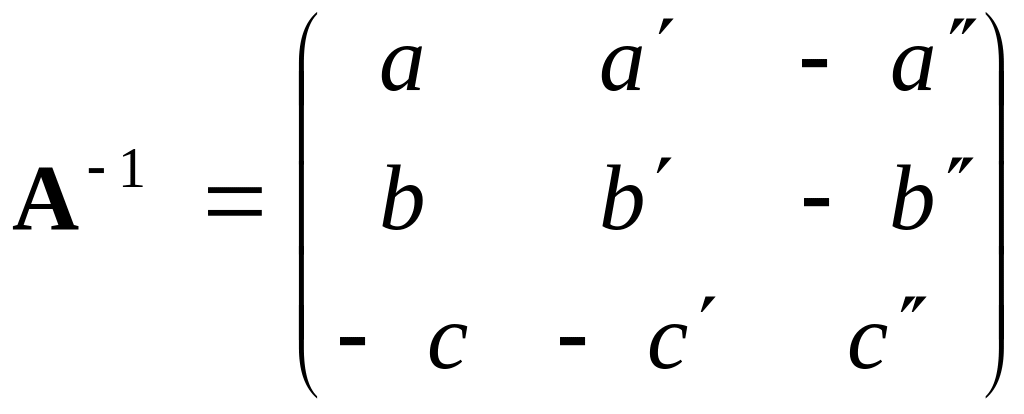З рівності (18) виводимо такі важливі залежності між елементами матриці А:

, ,

, , (19)

, .

З (19) слідують і такі співвідношення:

,

, (20)

.

Перемноживши обидві частини рівності (12) зліва на , дістанемо:

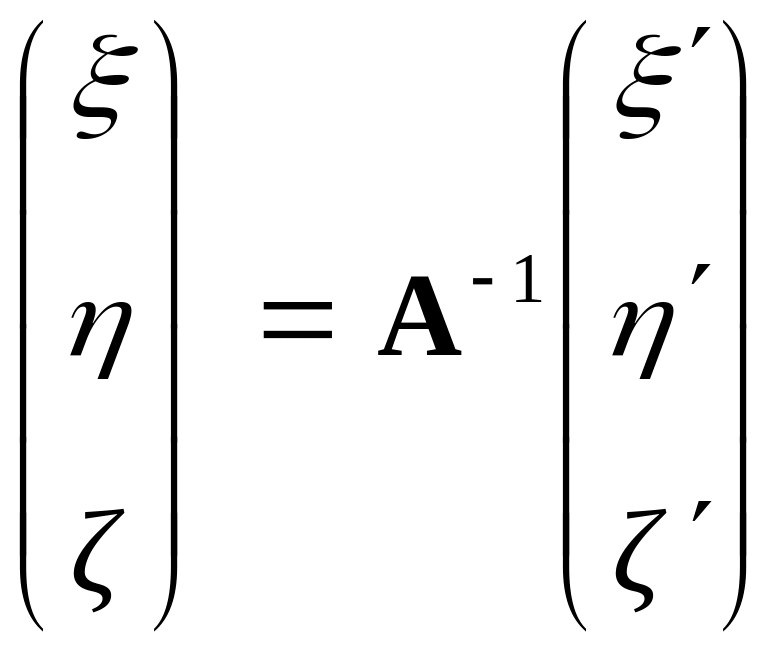. (21)

Отже, є матриця перетворення, оберненого щодо перетворення (12). Оскільки для точки O , , , то остання з рівностей (11) дає: . Звідси робимо висновок, що завжди

. (22)