3.2 Вимірювання відрізків на карті Бельтрамі

Нехай на осі η в площині (карта Пуанкаре) дано точку А₁ з ординатою . Побудуємо евклідове коло т радіуса 2 в півплощині так, щоб воно дотикалось до осі ξ в початку координат О (рис. 19); позначимо його центр че­рез М. Інверсія відносно кола т відображає півплощину на круг k радіуса 1, побудований на відрізку МО як на діаметрі. Нехай при цьому точка А₁ перетвориться в точку А'. Позначимо евклідову довжину відрізка ΩА', де Ω — центр круга k, через ρ. Тоді за властивістю інверсії відносно кола т

(4)

(5)

Від карти Пуанкаре, яку ми дістали на крузі k, перейдемо до карти Бельтрамі; нехай при цьому точка А' перетвориться в точку А. Позначивши евклідову довжину відрізка ΩА через ρ* і скориставшися з залежностей (3), (4), отримаємо:

Аналогічно для другої точки В, що є відображенням на карті Бельтрамі точки В₁, дістанемо:

Розглянемо тепер подвійне відношення (АВОМ) = (МОВА) чоти­рьох точок А, В, О, М прямої ОМ. З двох попередніх рівностей маємо:

Прологарифмуємо дану рівність:

Звідси

В силу формули (12) гіперболічна довжина від­різка А₁В₁, а отже, і відрізка АВ, дорівнює Звідси та з останньої рівності для гіперболічної довжини відрізка АВ дістанемо:

Якщо А, В — дві довільні точки гіперболічної площини (точки всередині круга Бельтрамі, (рис. 21), а X, Y — кінцеві точки хорди круга Бельтрамі, яка містить відрізок АВ, то гіперболічна довжина від­різка АВ визначається формулою:

(5)

Справді, за допомогою гіперболічного руху точки X, Y можна сумістити від­повідно з точками О, М; при цьому по­двійне відношення точок А, В, X, Y до­рівнюватиме подвійному відношенню їх образів, бо гіперболічний рух є проек­тивне перетворення. Отже, формула (5) справедлива.

У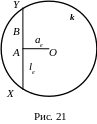 становимо тепер деякі залежності між евклідовими і гіперболічними довжинами відрізків. Гіпербо­лічну довжину відрізка ми будемо позначати малою латинською буквою, а евклідову довжину того ж відрізка на карті Бель­трамі — тією самою буквою з індексом _е.

Нехай кінець А відрізка АВ = а_e збігається з серединою хорди і точка В лежить між точками А і Y (рис. 21).

Тоді

Здійснимо ряд перетворень:

або

. (6)

Якщо XY є евклідів діаметр круга k, то точка А збігається з О, l_e = 1 і

(7)

3.3 Формули гіперболічної тригонометрії. Прямокутний трикутник.

Розглянемо довільний прямокутний трикутник. Перемістимо його за допомогою гіперболічного руху так, щоб вершини одного з його гострих кутів сумістилися з центром О круга Бельтрамі. Позначимо вершину другого гострого кута цього трикутника в його новому положення через В, вершину прямокутного трикутника — через С (рис. 22).

Введемо такі позначення:

, , , , ,

(Х — одна з точок перетину прямої ВС з колом круга Бельтрамі).

Зауважимо, що і в силу рівностей (6) і (7)

, ,

,

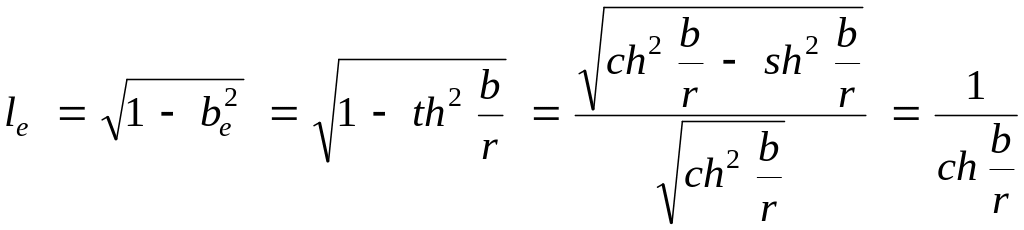З останньої рівності і з формули (6) одержимо:

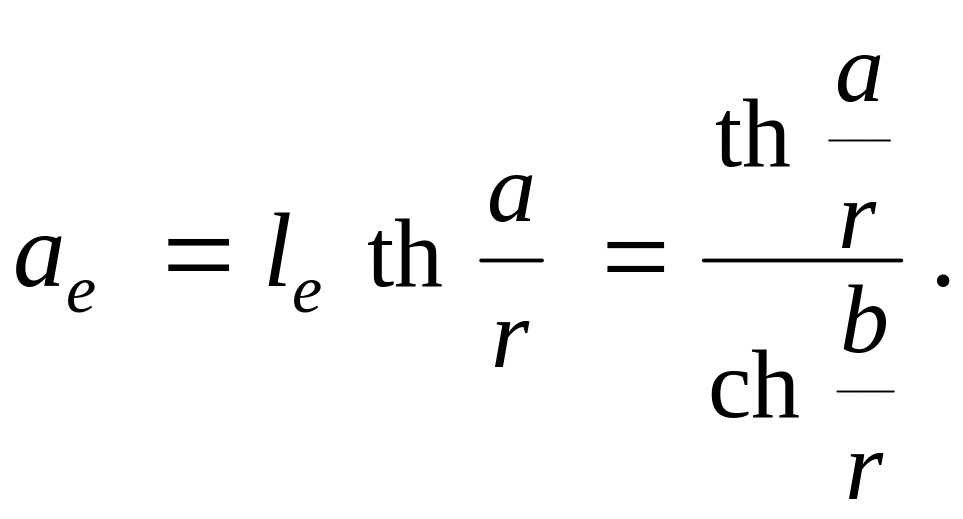
З допомогою цих рівностей можна встановити ряд залежностей між гіперболічними величинами елементів прямокутного трикутника OBC, використовуючи залежності між евклідовими величинами елементів цього трикутника.

Із співвідношення

Дістаємо:

або

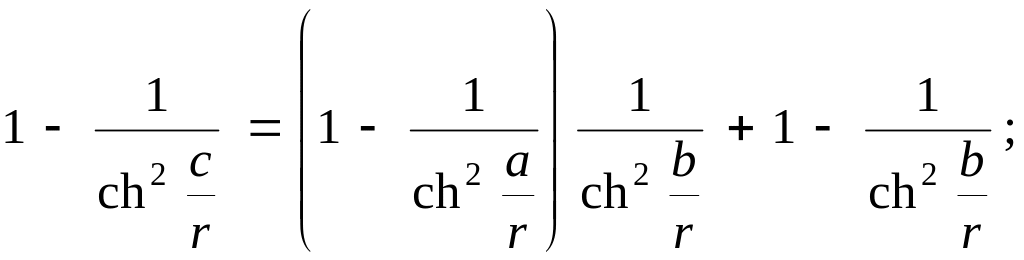
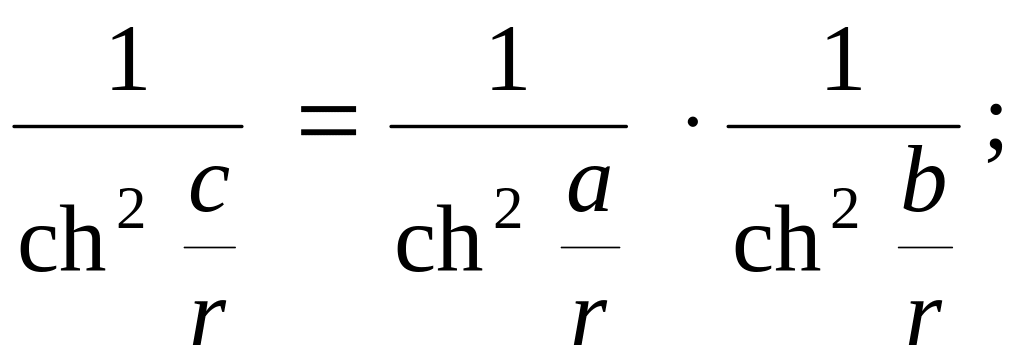
звідси

(8)

_{Із співвідношення сторін у прямокутному трикутнику}

дістаємо:

;

або

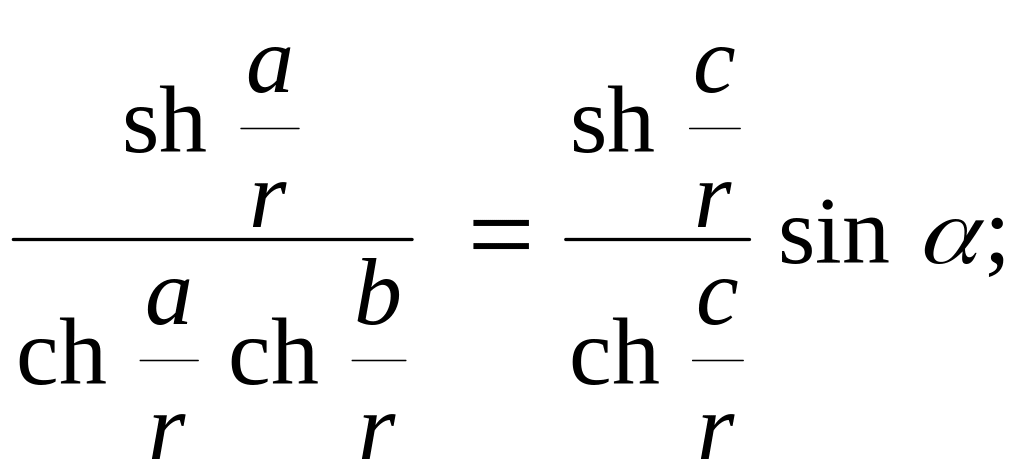
а скориставшись формулою (8), будемо мати:

(9)

_{Співвідношення}

дає

(10)

_{Співвідношення}

дає

(11)

Аналогічно з рівністю (9) маємо:

;

отже, рівності (11) можна надати вигляду:

;

Поділимо останню рівність почленно на рівність (9), будемо мати:

.

Звідси

. (12)

З рівності (10) маємо:

.

Аналогічно:

.

Отже,

Або в силу формули (9)

. (13)

У виведених вище формулах можна одночасно замінити a на b, α на β, b на a, β на α. Приєднавши одержані рівності до формул (8) — (13), отримаємо повний список основних залежностей між елементами прямокутного трикутника:

(14)

, (15)

, (16)

, (17)

, (18)

, (19)

, (20)

, (21)

, (22)

. (23)

Знайдемо ще залежність між евклідовою і гіперболічною величинами кута, (наприклад β_e і β). Нехай одна із сторін цього кута проходить через центр круга Бельтрамі.

З трикутника OCB (рис. 22) отримаємо:

.

За формулою (24)

отже,

. ()

Звідси можна зробити висновок, що , коли β — гострий кут.

П окажемо ще одну залежність, яку встановив М. І. Лобачевський, а саме, залежність між віддалю a і відповідним їй кутом паралельності П(α). Нехай вершина A рямокутного трикутника AOB лежить на колі круга Бельтрамі (рис. 23 ). Тоді BA || ОA, , .

Зробивши в формулі (20) граничний перехід, отримаємо:

. (26)

Звідси

, . (27)

З (26) маємо:

,

.