2. 3 Карта Пуанкаре.

Неважко довести, що півплощину , її точки і гіперболічні прямі можна відповідно трактувати як образи гіперболічної площини, її точок і прямих. Для доведення досить упевнитися, що вказана система об’єктів задовільняє вимоги всіх площинних аксіом геометрії Лобачевського. Побудована таким способом інтерпретація гіперболічної площини була запропонована відомим французьким математиком А. Пуанкаре.

Покажемо, що на карті Пуанкаре виконується аксіома паралельності Лобачевського:

Через точку А, що лежить поза гіперболічною прямою а, можна провести принаймні дві гіперболічні прямі, що не перетинають а.

Побудова очевидна з рис. 14; при цьому гіперболічні прямі b і с паралельні гіперболічній прямій а в різних її напрямах, а гіперболічні прямі а і d розбіжні.

Одне з важливих значень інтерпретації Пуанкаре полягає в тому, що вона дає можливість звести доведення будь-якої теореми гіперболічної геометрії до доведення деякого твердження евклідової геометрії. Розглянемо, наприклад, теорему:

Дві розбіжні прямі мають один і тільки один спільний перпендикуляр.

Рис. 14. Рис. 15.

Н а карті Пуанкаре дві розбіжні прямі зображуються у вигляді евклідових півкіл а і b з центрами на осі ξ, що не мають спільних точок (рис. 15). Отже, треба довести, що в півплощині існує єдине евклідове півколо c, ортогональне до осі ξ (бо воно є гіперболічною прямою) і до півкіл а, b. Очевидно, центром шуканого півкола с є точка перетину М осі ξ з радикальною віссю півкіл а, b, а його радіусом — евклідова дотична, проведена з М до а або b.

Якщо евклідові півкола а, b — концентричні, то с проходить через їх спільний центр і вироджується в е вклідову півпряму, перпендикулярну до осі ξ (рис. 16).

Можна також отримати модифікацію карти Пуанкаре (рис. 17 ), якщо відобразити півплощину на круг за допомогою інверсії. За центр інверсії потрібно взяти точку півплощини , щоб образ півплощини не містив нескінченно віддалених точок. При цьому вісь ξ перейде в евклідове коло ξ', точки півплощини — в точки круга ξ', гіперболічні прямі — в дуги евклідових кіл, ортогональних до кола ξ', гіперболічні кола — в евклідові кола, що цілком лежать у крузі ξ'. Точки кола ξ' відповідають нескінченно далеким точкам гіперболічної площини.

§3. Карти гіперболічної площини в евклідовому просторі. Карта Бельтрамі

3.1 Перехід від карти Пуанкаре до карти Бельтрамі

Нехай гіперболічна площина відображена на евклідів круг К одиничного радіуса за методом Пуанкаре. Знайдемо таке відображення круга К на себе, при якому внутрішня відносно К дуга будь-якого евклідового кола а, ортогонального до кола k, що обмежує круг К, переходила б у спільну хорду кіл а і k. Інакше кажучи, побудуємо таку інтерпретацію гіперболічної площини, в якій гіперболічним прямим відповідають відрізки евклідових прямих.

Візьмемо центр О круга К за полюс і який-небудь промінь ОХ за полярну вісь. Положення точки Р круга К визначимо поляр­ними (евклідовими) координатами:

, .

Нехай шукане перетворення переводить Р у точку Р (φ*, ρ*).

Можливість шуканого перетворення випливає з таких мірку­вань. Оскільки кожний евклідів діаметр кола k повинен відобра­зитись на себе, то

. (1)

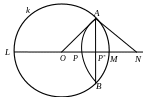
Рис. 18 Рис. 19

Але в такому випадку хорди АВ і СD кіл т і п. що прохо­дять через Р і ортогональні до k (рис. 18), повинні перетнутись в точці, яка лежить на промені ОР, що справді має місце, бо точки O, Р і друга спільна точка кіл т і п лежать на одній прямій — радикальній осі цих кіл, а радикальні осі ОР, АВ і СD кіл k, т, п, взятих попарно, перетинаються в одній точці — їх радикальному центрі.

Отже, залишається визначити ρ*, для чого досить, як видно з попереднього, скористатись тільки одним колом, що проходить через Р і ортогональне до k, — найзручніше тим, яке симетричне відносно ОР (рис. 19).

Позначимо його центр через N, радіус — через R, точки його перетину з k — через А, В і точки перетину ОР з k — через L, М. Оскільки точки L і М симетричні відносно кола m, то за властивістю інверсії

_;

_{Здійснимо ряд перетворень:}

_;

_;

Оскільки то

або

;

звідси

. (2)

Розглянемо прямокутні трикутники Δ ~ Δ . З співвідно-шення відповідних сторін цих трикутників отримаєм:

;

;

або, беручи до уваги (2):

. (3)

Отже, ми прийшли до нової інтерпретації гіперболічної площини, — інтерпретації, яку запропонував італійський математик Бельтрамі. Гіперболічна площина відображається на круг К, причому нескінченно далекі точки цієї площини перетворюються в точки кола k, а гіперболічні прямі — в хорди цього кола. Точки, що лежать поза k, відповідають ідеальним точкам гіперболічної площини, що грунтовніше буде з’ясовано нижче. Зокрема, точку, що лежить на продовженні евклідової хорди ХУ круга К, можна розглядати як ідеальну точку гіперболічної прямої ХУ.

Перетворення (1), (3) не є конформним; наприклад, коло, ортогональне до k, перетворюється в пряму, не ортогональну до k.

Зіставляючи інтерпретації Пуанкаре і Бельтрамі, ми помічаємо, що характерною особливістю першої є консерватизм кутів, другої — збереження прямолінійного розміщення точок.