2.2 Гіперболічні прямі півплощини

Гіперболічною прямою півплощини , метрика якої визначається рівністю (9), називається лінія, по якій в имірюється найкоротша віддаль між двома точками цієї півплощини. Доведемо, що вісь η є гіперболічною прямою.

Сполучимо точки А(0, η₁) і В(0, η₂) відрізком АтВ осі η і дугою АпВ якої-небудь кривої, що проходить через ці точки (рис. 7). Оскільки при тому самому значенні η величина

має на відрізку АтВ менше значення, ніж на дузі АпВ, то

що й треба було довести.

Обчислимо довжину відрізка АВ гіперболічної прямої , беручи до уваги, що на осі η . Проінтегруємо рівність (1)

.

Отже, довжина відрізка АВ гіперболічної прямої , обчислюється за формулою:

(6)

З останньої рівності можна зробити висновок, що гіперболічна пряма має дві нескінченно далекі точки: початок координат О системи ξ, η, і нескінченно далеку точку осі η в евклідовому розумінні.

Гіперболічними прямими є також ті евклідові півпрямі півплощини , які мають вершини на осі ξ і перпендикулярні до неї, і ті евклідові півкола цієї ж півплощини, які ортогональні до осі ξ і отже, мають центри на цій осі.

Рис. 8 Рис. 9

Справді, евклідову півпряму а за допомогою паралельного перенесення (1) можна сумістити з півпрямою (рис. 8), причому точка суміщається з точкою О; звідси, можна зробити висновок, що всі точки осі ξ є нескінченно далекими точками півплощини при наявності метрики, що визначається рівністю (9). Евклідове півколо b, ортогональне до осі ξ, можна за допомогою трансляції (паралельного перенесення) (1) перетворити в півколо b₁ що теж ортогональне до осі ξ і проходить через точку О (рис. 9); після цього, застосовуючи (3), перетворюємо b₁ в евклідову півпряму b₂, перпендикулярну до осі ξ, бо інверсія відносно одиничного кола k переводить b₁ у півпряму b', а дзеркальне відображення відносно осі η переводить b' в b₂.

Доведемо кілька важливих тверджень.

1. Дві точки півплощини визначають одну і тільки одну гіперболічну пряму

Якщо дані точки А, В лежать на евклідовій прямій, перпендикулярній до осі ξ, то евклідова півпряма АВ, вершина якої лежить на осі ξ, буде шуканою гіперболічною прямою (рис. 10). В іншому випадку знаходимо точку М, в якій евклідова медіатриса відрізка АВ перетинає вісь, і описуємо з М, як з центра, радіусом МА евклідове півколо (той самий рисунок); воно буде шуканою гіперболічною прямою.

Припустимо тепер, що через точки А і В проходить ще одна гіперболічна пряма b, відмінна від побудованої нами гіперболічної прямої а. Сумістимо а гіперболічним рухом з віссю η; нехай при цьому b, А, В перейдуть відповідно в b', А', В'. Розглянемо два випадки: відрізки АВ гіперболічних прямих а і b 1) не суміщаються, 2) суміщаються один з одним.

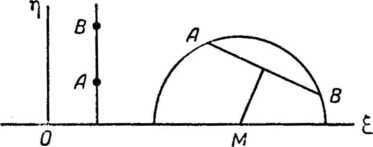
Рис. 10 Рис. 11

В першому випадку відрізки А'В' гіперболічних прямих η і b' не суміщаються один з одним, що, як ми бачили вище, неможливо. В другому випадку візьмемо на b' точку С', що не лежить на осі η (рис. 11).

Нехай В' лежить між А' і С'. Проведемо через точки А' і С' евклідове півколо, ортогональне до осі ξ; воно визначає таку гіперболічну пряму, що її відрізок А'С' відмінний від відрізка А'С' гіперболічної прямої b'. Отже, цей випадок зводиться до попереднього.

Із сказаного випливає, що дві різні точки півплощини визначають тільки одну гіперболічну пряму.

2. Якщо при гіперболічному русі дві точки гіперболічної прямої не змінюють свого положення, то жодна точка цієї гіперболічної прямої не змінює свого положення, бо в іншому випадку змінилася б віддаль якоїсь точки даної гіперболічної прямої принаймні від однієї з даних точок.

3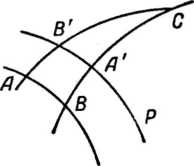 . Якщо при гіперболічному русі три точки А, В, С, що не лежать на одній гіперболічній прямій, не змінюють свого положення, то жодна точка гіперболічної площини не змінює свого положення.

Р

Рис. 13

озглянемо довільну точку Р гіперболічної площини, відмінну від точок А, В, С. Проведемо через Р гіперболічну пряму так, щоб вона перетинала дві сторони трикутника АВС, наприклад, гіперболічні прямі АС і ВС, і позначимо точки перетину відповідно через В' і А’ (рис. 13). В силу твердження 2 точки А’ і В', отже, і точка Р залишаються нерухомими.