1.3 Прямокутні координати. Диференціал дуги в прямокутних координатах

Прямокутними координатами точки Р відносно системи взаємо перпендикулярних осей ОХ, ОY ми назвемо: абсцисою Х точки Р — довжину проекції OQ радіус-вектора цієї точки на вісь ОХ, взяту зі знаком «+» або «-» залежно від того, чи лежить точка Q на промені ОХ, чи на його продовженні; оординатою Y точки Р — довжину перпендикуляра QР, опущеного з даної точки на вісь ОХ, взяту зі знаком «+» або «-» залежно від того, чи розміщена проекція R точки Р на вісь ОY на промені ОY, чи на його продовженні (рис. 47).

Встановимо залежності між вейєрштрасовими і прямокутними координатами точки Р. Координату η нам відомо: . Далі, з прямокутного трикутника OPQ знаходимо:

,

а з попередніх рівностей і тотожності визначається ξ.

Остаточно маємо:

,

(9)

Знайдемо диференціал дуги в прямокутних координатах. З попередніх формул знаходимо:

,

Звідси на підставі рівності (6) знаходимо:

(10)

1.4 Довжина кола. Довжина дуги еквідистанти і граничної лінії

Рівняння кола радіуса R з центром у полюсі має вигляд: .Звідси і з рівності (8) будемо мати:

Отже, довжина s кола радіуса R може бути обчислена за формулою:

(11)

В граничному випадку при з (11) дістанемо: , як і повинно бути в евклідовій геометрії.

Розглянемо еквідистанту, точки якої рівновіддалені від осі ОХ і знаходяться від неї на відстані a. Рівняння цієї еквідистанти має вигляд: . Звідси та з формули (10) маємо:

(12)

Якщо початкова і кінцева точка дуги еквідистанти мають відповідно абсциси Х₁ і Х₂, то з (12) для довжини s цієї дуги дістанемо:

Знайдемо тепер довжину дуги граничної лінії. Для цього скористаємось рівнянням (72) попереднього розділу:

_,

_{Підставимо замість ζ і ξ їх значення з формул (9), отримаємо}

_{Отже, рівняння граничної лінії в прямокутних координатах буде мати вигляд:}

або

. (13)

Диференціюючи це рівняння, отримаємо:

Звідси та з (10) маємо:

або

Отже, довжина s дуги граничної лінії (13) від початку координат до точки з ординатою Y визначається за формулою:

§2. Деякі плоскі криві в геометрії Лобачевського

2.1 Дотична і нормаль до плоскої кривої

Нехай плоска крива задана параметричним рівнянням у вейєрштрасових координатах:

, , . (1)

Рівняння прямої, що проходить через точки Р(ξ, η, ζ) і Р'(ξ+Δξ, η+Δη, ζ+Δζ) кривої (1), має вигляд:

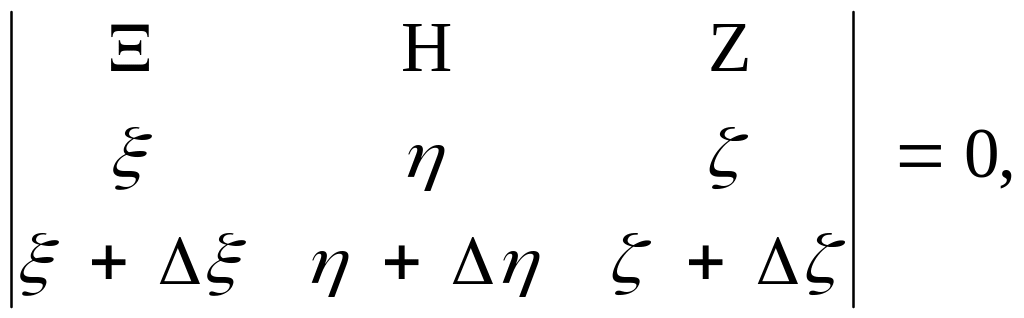
де Ξ, Н, Z — поточні координати точки, що належить прямій РР'. У визначнику, що стоїть в лівій частині останньої рівності, віднімемо від елементів третього рядка відповідні елементи другого рядка, після цього поділимо елементи третього рядка на Δt і перейдемо до границі при Δt = 0. В результаті дістанемо рівняння дотичної до кривої (1) в точці Р:

(2)

або

. (3)

Нехай рівняння нормалі до кривої (1) в точці Р є:

(4)

Точка Р належить прямій (4), тому

(5)

Умовою перпендикулярності прямих (1) і (4) є:

(6)

Виключивши u, v, w з (4), (5) і (6) дістанемо рівняння шуканої нормалі:

(7)