
- •Інтерпретація гіперболічної геометрії в евклідовому просторі
- •§1. Псевдосфера
- •Про моделі площини Лобачевського
- •Кривизна псевдосфери
- •Відображення псевдосфери на евклідову площину
- •§2. Карти гіперболічної площини в евклідовому просторі. Карта Пуанкаре
- •2.1 Гіперболічні рухи півплощини площини
- •2.2 Гіперболічні прямі півплощини
- •2. 3 Карта Пуанкаре.
- •§3. Карти гіперболічної площини в евклідовому просторі. Карта Бельтрамі
- •3.1 Перехід від карти Пуанкаре до карти Бельтрамі
- •3.2 Вимірювання відрізків на карті Бельтрамі
- •3.3 Формули гіперболічної тригонометрії. Прямокутний трикутник.
- •3.4 Формули гіперболічної тригонометрії. Косокутний трикутник.
- •Розділ іі аналітична геометрія на площині лобачевського
- •§1. Координати точки. Різні випадки рівняння прямих
- •1.1 Полярні, веєрштрасові та однорідні координати точки
- •1.2 Перетворення координат.
- •1.3 Загальний випадок перетворення координат.
- •1.4 Пряма
- •Інваріанти перетворення координат.
- •Про перетин двох прямих
- •Рівняння прямої, що проходить через дві дані точки
- •Координати середини відрізка
- •9 Про уявні точки та прямі
- •§2. Криві другого порядку
- •1.1 Криві другого порядку і другого класу
- •Класифікація кривих другого порядку
- •1.3 Рівняння граничної лінії
- •Розділ ііі початки диференціальної геометрії гіперболічної площини
- •§1. Вейєрштрасові, полярні та прямокутні координати
- •1.1 Диференціал дуги. Вейєрштрасові координати
- •1.2 Диференціал дуги. Полярні координати
- •1.3 Прямокутні координати. Диференціал дуги в прямокутних координатах
- •1.4 Довжина кола. Довжина дуги еквідистанти і граничної лінії
- •§2. Деякі плоскі криві в геометрії Лобачевського
- •2.1 Дотична і нормаль до плоскої кривої
- •2.2 Кривина плоскої кривої
- •2.3 Орициклоїда
- •2.4 Трактриса та її еволюта
1.3 Рівняння граничної лінії
Виведемо рівняння граничної лінії, взявши за початок координат і за вісь абсцис відповідно точку О даної граничної лінії і її вісь OX.
З означення граничної лінії випливає, що полярні координати φ, ρ точки Р цієї лінії зв’язані залежністю:
![]()
Звідси
на підставі рівності 26 з пункту 3.3 при
![]() дістанемо:
дістанемо:
![]()
Визначимо тепер вейєрштрасові координати ξ, η, ζ точки Р:
![]() ,
,
![]() ,
,
![]() .
.
Виключаючи звідси ρ, дістанемо рівняння граничної лінії у вейєрштрасових координатах:
![]() (72)
(72)
Для того, щоб знайти рівняння граничної лінії в однорідних координатах, піднесемо обидві частини останньої рівності до квадрата і після цього замінимо одиницю на . Після спрощення отримаємо:
![]() (73)
(73)
Звідси остаточний вигляд цього рівняння в однорідних координатах буде таким:
![]() (74)
(74)
Якщо зробити трансляцію осі так, щоб початок координат збігся з точкою (sh a, 0, ch a), то рівняння (72) перейде в таке рівняння:
![]()
або
![]() (75)
(75)
Якщо криву другого порядку прийняти за напрямну конуса, вершина якого лежить поза площиною даної кривої, то побудований таким способом конус називається конусом другого порядку. Тому криві другого порядку гіперболічної площини, так само як і криві другого порядку гіперболічної площини називаються конічними перерізами.
Розділ ііі початки диференціальної геометрії гіперболічної площини
§1. Вейєрштрасові, полярні та прямокутні координати
1.1 Диференціал дуги. Вейєрштрасові координати
Нехай
координати точок якоїсь кривої
(вейєрштрасові, полярні або інші)
виражаються неперервними функціями
параметра t
і нехай точкам A
i
B
цієї кривої відповідають значення
![]() і
і
![]() параметра
t.
При зростанні t
від
до
параметра
t.
При зростанні t
від
до
![]() точка кривої пробігає якусь криву AB.
Значенням:
точка кривої пробігає якусь криву AB.
Значенням:
![]()
відповідають точки:
![]() (1)
(1)
дуги
AB.
Сполучаючи точки (1) послідовно відрізками
прямих, дістанемо ламану лінію
![]() .
Якщо існує границя периметра цієї
ламаної при наближенні її сторін до
нуля, то ця границя береться за довжину
дуги AB.
.
Якщо існує границя периметра цієї
ламаної при наближенні її сторін до
нуля, то ця границя береться за довжину
дуги AB.
Припустимо, що крива, яку ми розглядаємо, задана периметричними рівняннями:
![]() ,
,
![]() ,
,
![]() ;
(2)
;
(2)
Поклавши
в рівностях (2)
![]() ,
дістанемо вейєрштрасові координати
ξі,
ηі,
ζі
точки Aі.
Позначимо:
,
дістанемо вейєрштрасові координати
ξі,
ηі,
ζі
точки Aі.
Позначимо:
![]()
![]()
![]()
![]()
На підставі формули (43) попереднього розділу, не прирівнюючи r до одиниці, дістанемо:
 (3)
(3)
Далі з тотожності
![]() ,
,
яку можна записати так:
![]() ,
,
дістанемо:
![]() .
.
Із (3) і (4) маємо:
![]() .
(5)
.
(5)
Якщо
![]() ,
то
,
то
![]() ,
і тому з (5) дістанемо:
,
і тому з (5) дістанемо:
![]() ,
,
де
![]() —
нескінченно мала величина. Тому в
рівності
—
нескінченно мала величина. Тому в
рівності
![]()
друга
сума правої частини наближається до
нуля, якщо всі різниці
![]() необмежено спадають, а перша сума правої
частини має границею інтеграл:
необмежено спадають, а перша сума правої
частини має границею інтеграл:
 ,
,
що визначає довжину дуги AB. Звідси, зокрема робимо висновок, що диференціал дуги ds визначається рівністю:
![]() .
(6)
.
(6)
1.2 Диференціал дуги. Полярні координати
Із залежностей між полярними координатами φ, ρ і вейєрштрасовими
ξ, η, ζ:
![]()
![]()
![]()
дістаємо:
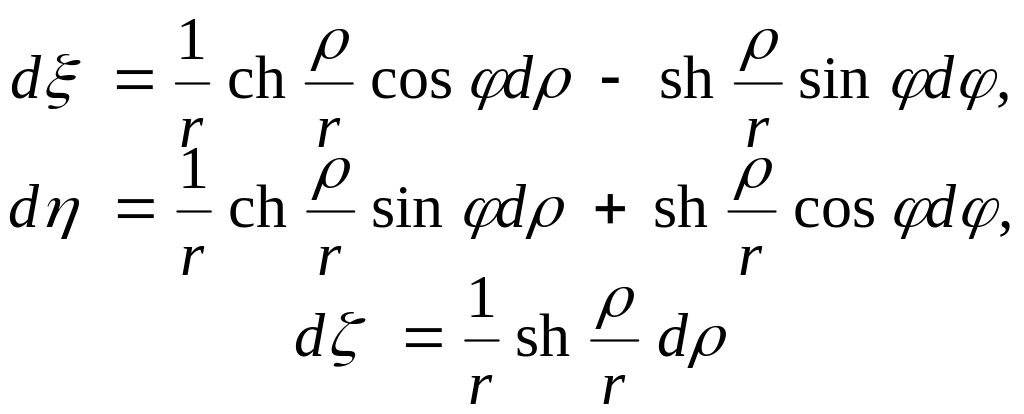 (7)
(7)
Із (6) і (7) маємо:
![]() .
(8)
.
(8)
