§2. Криві другого порядку

1.1 Криві другого порядку і другого класу

Кривою другого порядку ми назвемо множину точок (х; у; z), однорідні координати яких задовольняють рівняння:

(60)

Всяка пряма (61)

має з кривою (60) дві спільні точки; якщо ці точки суміщаються, то кажуть, що пряма (61) дотикається до кривої (60).

Кривою другого класу ми назвемо множину прямих (и: v: w), однорідні координати яких и, v, w задовольняють рівняння:

(62)

Через кожну точку (х; у; z) проходять дві прямі з числа тих, які утворюють криву (62); якщо ці прямі суміщаються, то кажуть, що точка (х; у; z), належить кривій (62).

З попереднього виходить, що в рівнянні кривої роль змінних величин будуть відігравати координати точок цієї кривої, коли ми розглядаємо її як множину точок, і координати дотичних до кривої, коли ми розглядаємо її як множину прямих.

Доведемо, що крива другого порядку є разом з тим кривою другого класу. Перетворимо рівняння (60) до змінних и, v, w, припускаючи, що пряма дотикається до даної кривої. Виключаючи z з рівнянь (60) і (61), дістанемо:

(63)

Рівняння (63) має кратний корінь, тому

або, вважаючи :

(64)

або

Рівність (64) крім того, що вона є умовою дотику прямої до кривої, також являє собою рівняння кривої (60) в координатах прямої. Оскільки ми дістали рівняння другого степеня, то крива (60) є кривою другого класу. Аналогічно доводиться, що крива другого класу є разом з тим кривою другого порядку.

Множина нескінченно далеких точок гіперболічної площини, що визначається рівнянням

(65)

і називається абсолютом гіперболічної площини, є кривою другого поряд­ку. Користуючись рівністю (64), легко знаходимо рівняння абсолюта в координатах прямої:

(66)

Звідси ясно, що прямі, однорідні координати яких задовольняють рівність (66), утворюють множину дотичних до абсолюта.

2. Класифікація кривих другого порядку

Обмежуючись розглядом влас­них дійсних кривих, що не вироджуються в прямі, ми візьмемо за критерій класифікації кривих другого порядку характер спільних точок кривої і абсо­люта (абсолютні точки кривої) і спільних дотичних кривої і абсолюта (абсолютні дотичні кривої). Перші можна визначити, розв'язуючи спільно рівняння (60) і (65), другі — розв'язуючи спільно рівняння (64) і (66).

Для надання наочності питанню ми будемо розглядати рівняння (60) і (64) як рівняння конічних перерізів евклідової площини в однорідних координатах точки або відповідно в однорідних координатах пря­мої, беручи за основу прямокутну систему координат. При тій же умові рівняння (65) і (66) визначають те саме евклідове коло одиничного радіуса з центром у початку координат, причому точки цього кола відпо­відають нескінченно далеким точкам гіперболічної пло­щини, а дотичні до нього — дотичним до абсолюта гіперболічної площини. Далі, точки, що лежать все­редині або поза кругом, обмеженим цим колом, зобра­жають відповідно власні й ідеальні точки гіперболіч­ної площини. Нарешті, рівняння (60) і (64) визначають в евклідовій площині той самий конічний переріз.

Доведемо, що ця інтерпретація гіперболічної пло­щини збігається з інтерпретацією Бельтрамі. Побудуємо евклідову прямокутну систему координат XY з початком координат в евклідовому центрі точки O кола k (рис. 34). Нехай x_e, y_e, z_e — евклідові однорідні координати точки P, так що

,

і нехай φ_е, ρ_е — евклідові полярні координати тієї ж точки.

Виходячи з інтерпретації Бельтрамі, позначимо вейєрштрасові, полярні і однорідні гіперболічні полярні координати точки P відповідно через ξ, η, ζ, φ, ρ і x, y, z. Тоді

,

Далі,

(67)

(68)

Внаслідок цього

x_e : y_e : z_e = x : y: z (69)

тобто в цьому випадку однорідні евклідові координати точки P можна одночасно розглядати і як однорідні гіперболічні координати цієї точки.

Користуючись цією інтерпретацією, ми можемо встановити такі типи кривих другого порядку:

1. Опукла гіпербола (рис. 35). Чотири дійсні абсолютні точки; чотири уявні абсолютні дотичні.

2. Угнута гіпербола (рис. 36). Чотири дійсні абсолютні точки; чотири дійсні абсолютні дотичні.

3. П івгіпербола (рис. 37). Дві дійсні і дві уявні абсолютні точки; дві дійсні і дві уявні абсолютні дотичні.

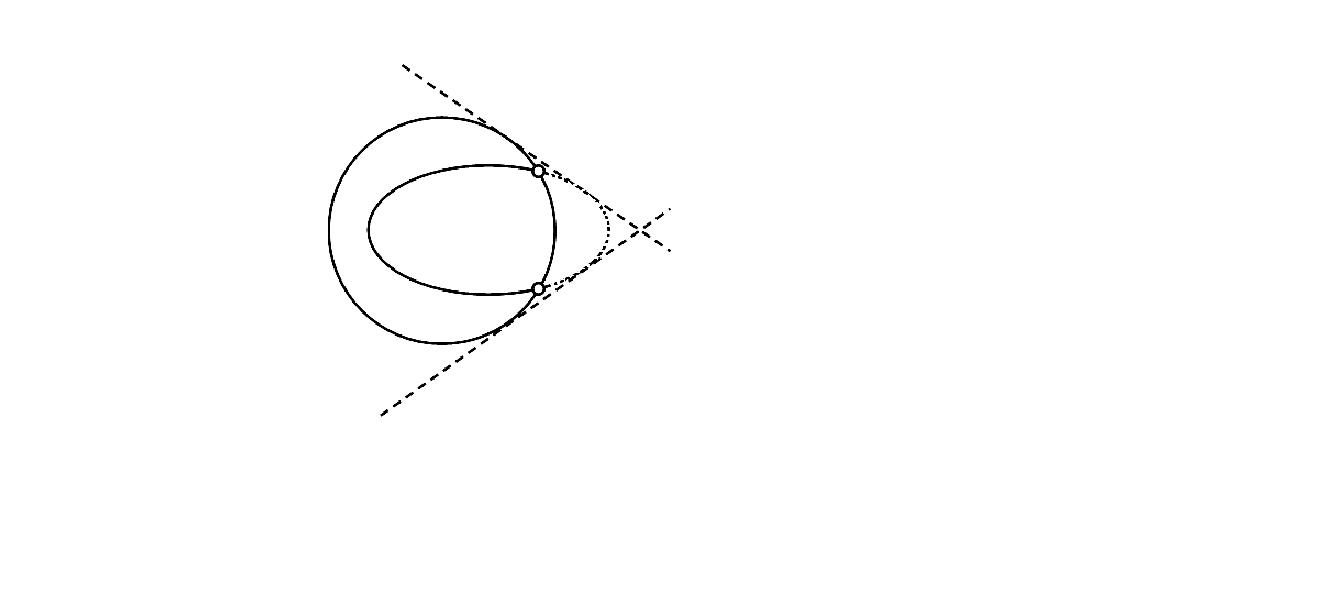
Рис. 35 Рис. 36 Рис. 37

4. Еліпс (рис. 38). Чотири уявні абсолютні точки; чотири уявні абсолютні дотичні.

5. Угнута гіперболічна парабола (рис. 39). Дві пристайні і дві дійсні різні абсолютні точки; дві пристайні і дві дійсні різні абсолютні дотичні.

6. Опукла гіперболічна парабола (рис. 40). Дві пристайні і дві дійсні різні абсолютні точки; дві пристайні і дві уявні комплексно спряжені абсолютні дотичні.

Рис. 38 Рис. 39 Рис. 40

7. Еліптична парабола (рис. 41). Дві пристайні і дві уявні комплексно спряжені абсолютні точки; дві пристайні і дві уявні комплексно спряжені абсолютні дотичні.

8. Стична парабола (рис. 42). Чотири дійсні абсолютні точки, три з яких збігаються; Чотири дійсні абсолютні дотичні три з яких збігаються.

9. Еквідистанта (рис. 43). Дві пари пристайних абсолютних точок; дві пари пристайних абсолютних дотичних.

Рис. 41 Рис. 42 Рис. 43

10. Гранична лінія (рис. 44). Чотири пристайні абсолютні точки, чотири пристайні абсолютні дотичні.

11. Коло (рис. 45).

Рис. 44 Рис. 45

Виведемо рівняння кола. Нехай радіус кола k дорівнює R, а його центр M лежить на додатному напрямі осі OY на віддалі a від початку координат (рис. 46). Позначимо через φ, ρ полярні координати точки P цього кола. З трикутника ОМР отримаємо:

або беручи до уваги рівності (1):

Щоб надати цьому рівнянню однорідний вигляд, піднесемо його обидві частини до квадрата і помножимо праву частину на вираз , який є тотожно рівним одиниці:

. (71)