РОЗДІЛ І

Інтерпретація гіперболічної геометрії в евклідовому просторі

§1. Псевдосфера

1. Про моделі площини Лобачевського

Площина Лобачевського вивчає властивості «площини Лобачевського» (в планіметрії) і «простору Лобачевського» (в стереометрії).

Площина Лобачевського — це площина, в якій визначені прямі лінії, а також рухи фігур, і виконуються всі аксіоми евклідової геометрії, за винятком аксіоми про паралельні прямі, яка замінюється аксіомою Лобачевського: «Через точку поза прямою в площині можна провести принаймі дві прямі, які не перетинають даної».

Для доведення несуперечливості системи аксіом користуються методом створення моделей. З розвитком і введенням в математику аксіоматичного методу, під інтерпретацією (або моделлю) деякої системи аксіом стали розуміти систему визначених об'єктів і відношень між ними, в яких дана система аксіом знаходить своє реальне втілення. [2, с.110]. При цьому вважають, що якщо для деякої системи аксіом існує або можна побудувати інтерпретацію (модель), то ця система аксіом несуперечлива, тобто, не тільки самі аксіоми, а й будь-які теореми, на них логічно грунтуються ніколи не можуть суперечити одна одній.

Є декілька класичних ізометричних (таких, що зберігають відстань між точками) моделей (інтерпретацій) площини Лобачевського, що мають гаусову кривину К = -1:

• Інтерпретація Бельтрамі в крузі;

• Інтерпретація Бельтрамі гіперболічної геометрії на псевдосфері;

• Евклідова модель Келлі-Клейна;

• Проективна модель Келлі-Клейна;

• Інтерпретація Пуанкаре на півплощині;

• Інтерпретація Пуанкаре всередині круга.

Найпершою була інтерпретація італійського математика Бельтрамі, який показав, що геометрія на частині площини Лобачевського співпадає з геометрією на поверхнях постійної від'ємної кривини.

У 1878 р. Ф. Клейн побудував таку модель, в якій за площину Лобачевського приймається внутрішність деякого круга К (без граничного кола). Точки розглядаються на цій моделі, в звичайному розумінні, а прямі — як довільні хорди (кінцеві точки виключені). Цю інтерпретацію також називають інтерпретацією Бельтрамі-Клейна (рис. 1). За формулою Клейна на цій моделі можна обчислювати відстані між точками, вимірявши підходящі відрізки на моделі.

М одель Пуанкаре — модель простору Лобачевского, запропонована Анрі Пуанкаре в 1882 р. в зв’язку з задачами теорії функцій комплексної змінної. Модель Пуанкаре примітна тим, что в ній кути зображуются звичайними кутами (тобто модель Пуанкаре конформна, навідміну від моделі Клейна. За площину Лобачевського приймається внутрішність круга (рис. 2) в евклідовому просторі; граничне коло називається «абсолютом». Роль прямих виконують дуги кіл (a,b,b'), перпендикулярних до абсолюту, що містяться в цьому крузі, а також його діаметри. В цій моделі даний круг зручно вважати одиничним кругом на комплексній площині. Модель Келлі – Клейна — перша модель всієї площини Лобачевского.

Еудженіо Бельтрамі, який знайшов модель для неевклідової геометрії, показав у своїй роботі «Досвід інтерпретації неевклідової геометрії» (1868), що поряд з площинами, на яких здійснюється евклідова геометрія, і сферичними поверхнями, на які діють формули сферичної геометрії, існує і така реальна поверхня, названа ним псевдосферою (рис. 3), на якій частково здійснюється планіметрія Лобачевського.

У

Рис. 3

цій праці було також встановлено, що в евклідовому просторі внутрішня геометрія поверхонь постійної гаусової кривини локально співпадає з геометрією Лобачевського. Роль прямих виконують геодезичні лінії (на кривій поверхні геодезичні лінії, замінюючи прямі, дозволяють будувати геометрію так, як це робиться на площині).

Проте на псевдосфері дається інтерпретація геометрії на обмеженій ділянці, а не на всій площині Лобачевського.

Псевдосферу можна отримати шляхом обертання трактриси навколо осі абсцис.

Т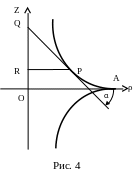 рактрисою називається евклідова крива, яка має ту властивість, що відрізок дотичної до неї, обмежений точкою дотику і точкою перетину дотичної з даною прямою а має сталу довжину (рис. 4).

Виведемо рівняння трактриси в площині ρZ, вважаючи, що точка трактриси, яка знаходиться на віддалі r, від осі Z, лежить на осі ρ, і що осі ρ і Z взаємно перпендикулярні.

Проведемо до трактриси дотичну в точці Р, вона перетне вісь Z в точці Q. Побудуємо PR OZ. Позначивши координати точки Р через ρ, z, а кут між віссю Оρ і дотичною до трактриси через α матимемо:

RP= ρ, PQ=r, , α= , .

Отже,

. (1)

Проінтегруємо останнє рівняння, і візьмемо до уваги, що при Отримаємо таке рівняння трактриси:

(2)

Вісь OZ для трактриси є асимптотою, і обертаючись навколо асимптоти трактриса опише поверхню – псевдосферу, рівняння якої

, (3)

Рівняння псевдосфери можна описати і в параметричному вигляді:

,

(4)

Зауважимо, що якщо в останньому рівнянні взяти ρ=const, то воно визначатиме паралелі псевдосфери (кола), а при φ=const — меридіани псевдосфери (трактриси).