Лабораторная работа №6 Механический расчет полукомпенсированной цепной контактной подвески

Цель работы: произвели механический расчет полукомпенсированной цепной контактной подвески.

6.1 Определение эквивалентного пролета анкерного участка

Для расчета выберем анкерный участок главного пути I станции длиной 1574 м. Эквивалентный пролет анкерного участка определяется по формуле, м

l_экв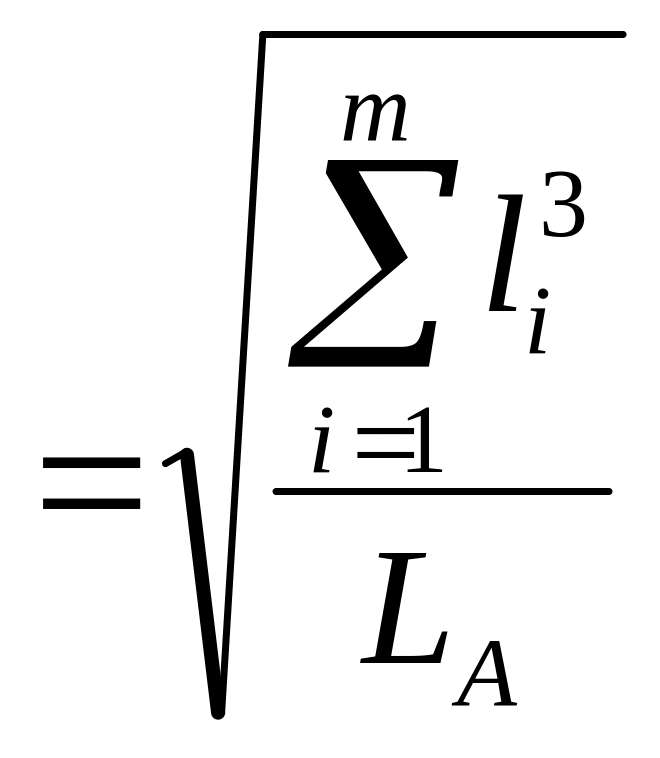 , (6.1)

где l_i – длина i-го пролета, м;

m – число пролетов в анкерном участке;

L_A – длина анкерного участка, м.

м.

Посчитав формулу (6.1) получаем, что эквивалентный пролет анкерного участка равен 62 м.

6.2 Определение исходного режима

Под исходным режимом при механическом расчете полукомпенсированной контактной подвески при заданных климатических условиях понимают такой режим температуры и нагрузки, при котором натяжение несущего троса достигает своего максимального значения, допускаемого по условиям прочности и другим ограничениям.

Максимальное натяжение несущего троса (Т_мах) может возникать как при минимальной температуре (режим t_min), так и при максимальной гололедной нагрузке при ветре, сопутствующем гололедообразованию (режим t_гv).

Исходный режим определим путем сравнения результирующей нагрузки на несущий трос (при гололеде с ветром) с критической нагрузкой. Величина критической нагрузки определяется по формуле, Н/м

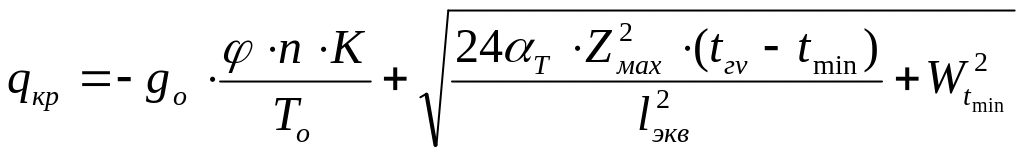, (6.2)

где – нагрузка от собственного веса цепной подвески, Н/м;

– номинальное натяжение контактного провода, Н;

– приближенное значение натяжения несущего троса при

температуре беспровесного положения контактного провода t_o, Н;

a_Т – коэффициент линейного расширения материала несущего троса, 1/^оС;

φ - конструктивный коэффициент цепной подвески, находится по формуле,

, (6.3)

где С – расстояние от опоры до ближайшей простой (нерессорной) струны,

С=(6…12) м соответственно для длин прлетов от 40 до 75 м;

- приведенная нагрузка цепной подвески при режиме

, (6.4)

где - приведенное натяжение цепной подвески.

. (6.5)

Рассчитаем конструктивный коэффициент цепной подвески

.

Определим приведенное натяжение цепной подвески

Н/м.

Определим приведенную нагрузку цепной подвески при режиме t_min

Н/м.

Определим значение критической нагрузки

Н/м.

Полученную по формуле (6.2) нагрузку q_кр сравниваем с нагрузкой q_гv.:

Т.к. q_кр < q_гv ,то за исходный режим принимаем режим гололеда с ветром, сопутствующим гололедообразованию.

6.3 Определение температуры беспровесного положения контактного провода

Температура беспровесного положения контактного провода определяется по формуле, ⁰С

(6.6)

где – максимальная температура, ^оС;

– минимальная температура, ^оС;

= 15 ^оС – поправочный коэфициент.

=(30-25)/2-15= -12,5 ^оС.