Увага!!!!
Під час пояснення теми «Розв’язання задач дробово-лінійного програмування симплексним методом» мною було пропущене одне обмеження (в системі обмежень приведеної до лінійного виду). Тому прошу уважно розв’язувати свої варіанти. В прикладах наведених в підручниках це обмеження є.
Індивідуальна робота №5
Варіант №1.
1. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму.
2. Розв’язати задачу дробово-лінійного програмування симплексним методом.
за умов
3. Розв’язати графічно задачу нелінійного програмування.
За умов
4. Розв’язати задачу ігрового моделювання графічно
Дві
конкуруючі фірми (гравці) реалізують
на ринок продукцію, що швидко псується.
Кожен із гравців хоче зайняти сегменти
ринку (стратегії). Відомі прибуток
(виграш) або збиток (програш) для кожного
сегмента ринку, які наведені в платіжній
матриці:
Знайти оптимальні стратегії й ціну гри кожного гравця і дати економічну інтерпретацію розв’язку.
Індивідуальна робота №5
Варіант №2
1. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму.
2. Розв’язати задачу дробово-лінійного програмування симплексним методом.
за умов
3. Розв’язати графічно задачу нелінійного програмування
4. Розв’язати задачу ігрового моделювання графічно
Дві
конкуруючі фірми (гравці) реалізують
на ринок продукцію, що швидко псується.
Кожен із гравців хоче зайняти сегменти
ринку (стратегії). Відомі прибуток
(виграш) або збиток (програш) для кожного
сегмента ринку, які наведені в платіжній
матриці:
Знайти оптимальні стратегії й ціну гри кожного гравця і дати економічну інтерпретацію розв’язку.
Індивідуальна робота №5
Варіант №3
1. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму.
,
.
2. Розв’язати задачу дробово-лінійного програмування симплексним методом.
за умов
3. Розв’язати графічно задачу нелінійного програмування.
4. Розв’язати задачу ігрового моделювання графічно
Дві
конкуруючі фірми (гравці) реалізують
на ринок продукцію, що швидко псується.
Кожен із гравців хоче зайняти сегменти
ринку (стратегії). Відомі прибуток
(виграш) або збиток (програш) для кожного
сегмента ринку, які наведені в платіжній
матриці:
Знайти оптимальні стратегії й ціну гри кожного гравця і дати економічну інтерпретацію розв’язку.
Індивідуальна робота №5
Варіант №4
1. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму.
,
.
2. Розв’язати задачу дробово-лінійного програмування симплексним методом.
за умов
3. Розв’язати графічно задачу нелінійного програмування.
4. Розв’язати задачу ігрового моделювання графічно
Дві
конкуруючі фірми (гравці) реалізують
на ринок продукцію, що швидко псується.
Кожен із гравців хоче зайняти сегменти
ринку (стратегії). Відомі прибуток
(виграш) або збиток (програш) для кожного
сегмента ринку, які наведені в платіжній
матриці:
.
Знайти оптимальні стратегії й ціну гри кожного гравця і дати економічну інтерпретацію розв’язку.
Індивідуальна робота №5
Варіант №5
1. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму.
,
.
2. Розв’язати задачу дробово-лінійного програмування симплексним методом.
за умов
3. Розв’язати графічно задачу нелінійного програмування.
4. Розв’язати задачу ігрового моделювання графічно
Дві
конкуруючі фірми (гравці) реалізують
на ринок продукцію, що швидко псується.
Кожен із гравців хоче зайняти сегменти
ринку (стратегії). Відомі прибуток
(виграш) або збиток (програш) для кожного
сегмента ринку, які наведені в платіжній
матриці:
.
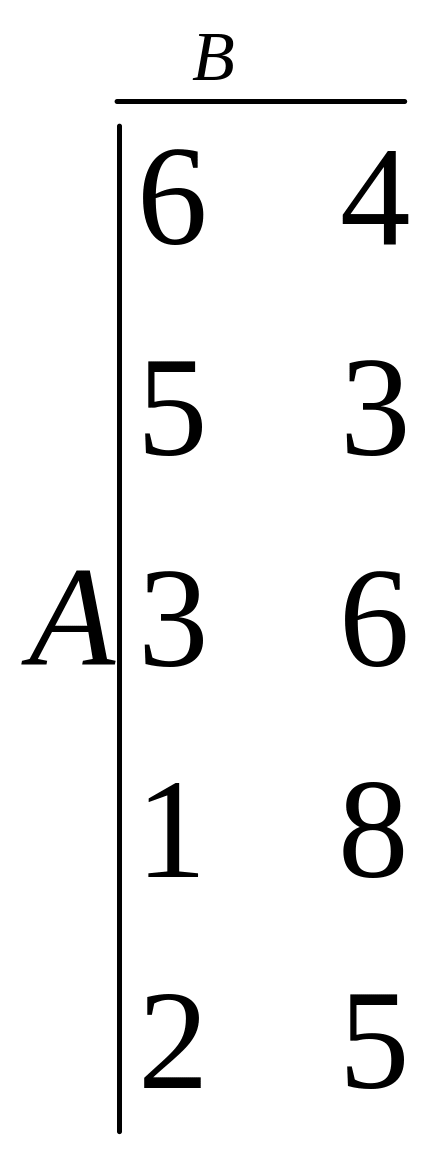Знайти оптимальні стратегії й ціну гри кожного гравця і дати економічну інтерпретацію розв’язку.