4.3. Линейная термодинамика – определение термодинамических сил, 2-ой и 3-ий законы Онзагера

Приведенный пример позволил понять, почему причины возникновения потоков в линейной термодинамике названы силами, точнее термодинамическими силами. В механическом аналоге термодинамической системы – механической диссипативной системе – обычная механическая сила и термодинамическая сила – просто одно и тоже (идентичны). Однако приведенные ранее экспериментально установленные законы (законы диффузии и теплопроводности, закон Ома) показывают, что причины возникновения потоков могут быть не связаны с механическими силовыми характеристиками системы. Что будут представлять собой термодинамические силы в этих случаях? Существует ли какое-либо правило определения термодинамических сил для рассматриваемой неравновесной системы?

Чтобы ответить на эти вопросы рассмотрим еще одну (модельную) диссипативную механическую систему, поведение которой демонстрирует поведение стандартной неравновесной термодинамической модели (этот пример подробно рассмотрен в учебнике А.А.Жуховицкого /4/, здесь он приводится в сокращенном варианте). В стеклянную емкость, заполненную вязкой жидкостью (например, глицерином или густым силиконовым маслом) помещено большое количество мелких железных шариков (дробинок). Посредством перемешивания шарики однородно распределены в жидкости. Вязкость жидкости и размеры шариков подобраны таким образом, чтобы за время проведения опыта не происходило заметного оседания шариков под действием силы тяжести (т.е. шарики не тонут, они взвешены в жидкости). Количество шариков в единице объема жидкости характеризуется величиной с [1/м³] – это фактически объемная концентрация шариков (частиц, молекул). Емкость с жидкостью и взвешенными в ней железными шариками помещена в однородное магнитное поле (рис.4.2)

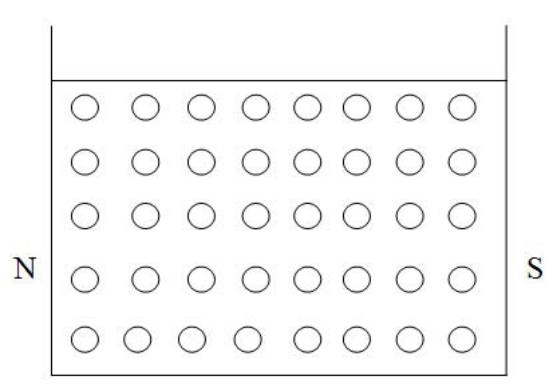
Рис.4.2. Емкость с вязкой жидкостью и взвешенными в ней железными шариками в однородном магнитном поле

Под действием внешнего магнитного поля шарики намагничиваются и начинают притягиваться к ближайшему магнитному полюсу. Сила притяжения – она имеет смысл механической силы X_N, которая действует на шарики со стороны магнитного поля – одинакова во всем объеме жидкости. Поскольку жидкость вязкая, скорость движения шариков одинакова - v - и не меняется со временем. Это означает, что вся затрачиваемая на перемещение шариков энергия, тратится на трение внутри жидкости. Напишем выражение для энергии dW, требуемой для движения шариков в единице объема жидкости за время dt

; . (4.13)

В правой части выражения (4.13) показано формирование размерности полученной величины, которая в результате приобретает смысл энергии в единице объема или объемной плотности энергии.

Следует учесть также, что произведение vc имеет размерность , т.е. размерность потока шариков I. Тогда уравнение (4.13) можно переписать в следующем виде

. (4.13а)

В результате движения шариков в вязкой жидкости вся энергия диссипирует, превращается в тепло, которое благодаря принципу локального равновесия может быть выражено через плотность энтропии

dW = δQ; δQ = Tds. (4.14)

После подстановки (4.13а) в (4.14) и деления обоих частей полученного уравнения на dt получим

, (4.15)

индекс «необ» при производной плотности энтропии по времени (скорости изменения энтропии при движении шариков) означает необратимость рассеяния энергии движения шариков, необратимость перехода ее в тепло.

Полученное соотношение показывает связь между скоростью изменения параметра, введенного в классической термодинамике, между скоростью изменения энтропии (плотности энтропии) и параметрами, характеризующими отклонение от равновесия – потоком («удельной» скоростью) и силой (причиной возникновения потока). Энтропия – понятие чисто термодинамическое. Поток и сила – это динамические понятия, которые могут использоваться для получения динамической картины процесса. Соотношение (4.15) связывает термодинамический (равновесный) и динамический подходы в описании неравновесной системы.

Очень заманчивым было стремление расширить соотношение связи между динамикой и термодинамикой на широкий круг неравновесных систем и процессов. Это сделал Онзагер, написав 2-ой закон линейной термодинамики – 2-ой закон Онзагера – в следующем виде

. (4.16)

2-ой закон Онзагера показывает, что скорость изменения плотности энтропии пропорциональна сумме произведений каждого из потоков, присутствующих в системе, на «свою» силу. Этот закон часто называют правилом определения термодинамических сил. Именно с помощью 2-го закона Онзагера можно находить явное выражение для термодинамических сил, если задана конкретная неравновесная система. Рассмотрим пример, который показывает, как это делается.

Пусть задана система, которая не включает в себя механических сил и соответствующих им потоков. Рассмотрим проводник в однородном электрическом поле E. Сечение проводника имеет площадь f. В электрическом поле вдоль проводника в направлении x протекает ток i . Будем считать, что этот проводник представляет собой нагревательный элемент в термическом устройстве (в печи сопротивления), и вся энергия электрического поля, которая расходуется на возбуждение электрического тока, переходит в тепло. Определим, сколько джоулевого тепла (т.е. тепла в соответствии с законом Джоуля-Ленца) за время dt выделяет элемент провода длиной dx

. (4.17)

Если учесть, что для провода с током данного объема V = fdx имеется термодинамическая связь выделяемого тепла с энтропией δQ = TdS, соотношение (4.17) можно переписать в виде

, (4.18)

и далее при делении обоих частей уравнения (4.18) на V получаем

, (4.19)

где s = S/V – плотность энтропии, а J = i/f – плотность тока. Плотность тока выражается как J = I_e∙e т.е. является произведением потока зарядов (электронов) I_e на величину единичного заряда (заряда электрона) e. Окончательно получаем

. (4.20)

При сравнении выражения (4.20) с 2-ым законом Онзагера легко заметить, что в правой части этого выражения записано произведение потока I_e (потока зарядов) на термодинамическую (электрическую) силу X_e = eE , которую в соответствии с электродинамикой можно выразить еще одним способом X_e = – e (φ – потенциал электрического поля).

Правило определения термодинамических сил (2-ой закон Онзагера) позволяет и в других случаях находить их вид. В химической системе, в которой отсутствуют «посторонние» силы, т.е. нет никаких других взаимодействий, кроме химических, при постоянстве объема и температуры (V = const, T = const) термодинамическая сила X_j , управляющая j – ым потоком (скоростью j – ой химической реакции) в данной системе, равна

X_j = – ΔG_j, (4.21)

т.е. определяется изменением энергии Гиббса в j – ой реакции.

В случае термодиффузии, когда в системе возникает поток тепла I_Q и поток i-го компонента вещества I_i , вывод выражений термодинамических сил также возможен. При помощи 2-го закона Онзагера удается найти вид тепловой силы X_Q и диффузионной силы X_i

. (4.22)

Итак, 1-ый и 2-ой законы Онзагера позволяют определить для рассматриваемой неравновесной системы при незначительных отклонениях от равновесия (область II диаграммы Бокштейна) термодинамические потоки и термодинамические силы и указывают на их линейную связь между собой. Каков дальнейший путь анализа неравновесных систем?

Алгоритм применения линейной термодинамики для описания неравновесных процессов следующий:

1. Определение потоков (и их размерностей), присутствующих в системе.

2. Определение термодинамических сил. Общую схему этой операции можно представить следующим образом:

- для исследуемой системы в заданных условиях необходимо записать термодинамическое локальное уравнение Гиббса;

- далее требуется привести уравнения непрерывности, характеризующие законы сохранения массы, энергии, заряда и т.д.;

- выражения для потоков, которые надо получить путем преобразования уравнений непрерывности, следует подставить в уравнение Гиббса и свести его к уравнению баланса для плотности энтропии

, (4.23)

где I_s – поток энтропии;

- сравнить полученное уравнение с 2-ым законом Онзагера и определить выражения для термодинамических сил.

3. Записать уравнения для потоков в системе в соответствии с 1-ым законом Онзагера. Решение полученной линейной системы позволяет определить неизвестные искомые величины. Коэффициенты Онзагера L_ik определяются из опытных данных или из модельных построений.

Здесь следует привести третий последний закон линейной термодинамики –3-ий закон Онзагера, – который имеет отношение к определению кинетических коэффициентов L_ik. Он является следствием принципа микрообратимости и формулируется следующим образом

L_ik = L_ki , (4.24)

что означает, что влияние i – ой силы на k – ый поток такое же, как k – ой силы на i – ый поток. Принцип микрообратимости (для химических процессов он соответствует принципу детального химического равновесия) утверждает, что в состоянии равновесия «любой молекулярный процесс и процесс, обратный этому процессу, протекают с одинаковой скоростью» (цитата из книги Б.С. Бокштейна «Диффузия в металлах» , М. 1978 г.). Таким образом, принцип микрообратимости и вытекающий из него 3-ий закон Онзагера требуют, как и все остальные базовые положения линейной термодинамики, существования локального равновесия. 3-ий закон Онзагера позволяет сократить число кинетических коэффициентов, входящих в уравнения 1-го закона. Это упрощает решение конкретных задач в рамках линейной термодинамики.