4. Термодинамические основы описания неравновесных систем

Первое, что надо сделать – это обосновать возможность адекватного применения термодинамического языка для описания неравновесных систем. Под термодинамическим языком здесь подразумевается весь математический аппарат термодинамики, все величины и параметры, входящие в используемые для расчетов соотношения и, самое главное, законы и постулаты, которые являются основанием всего здания термодинамики. Необходимость такого шага продиктована тем обстоятельством, что термодинамические понятия и все, что из них следует, привязано непосредственно к состоянию равновесия. Так, например, температура термодинамической системы при заданных условиях одинакова для всей системы, на этом основаны все расчеты для определения компонентного и фазового состава. Сами расчеты осуществляются с помощью законов, сформулированных для конкретных задач, но записанных для состояния равновесия. При рассмотрении неравновесных систем ситуация меняется, температура даже при неизменных внешних условиях может быть различной в разных частях системы. Причиной этого могут являться потоки (вещества или энергии), которые выводят систему из состояния равновесия и проходят через границы системы. Кроме того, внешние условия могут меняться со временем, скорость таких изменений не обязана быть бесконечно малой, чтобы сама система в каждый момент времени находилась в равновесии. Процессы релаксации в системе могут не поспевать за скоростью изменения внешних параметров. Необходимо введение некоторых дополнительных принципов, положений.

4.1. Принцип локального равновесия

Рассмотрим простую одномерную систему – скажем, нагревательное устройство – длинную трубчатую печь малого диаметра: длина L >> r , r – радиус печи. Пусть секция нагревателей печи, расположенная слева (рис. 4.1), включена и производит нагрев воздуха внутри печи. Секция нагревателей правой части печи отключена, воздух справа не греется. Через некоторое время после начала опыта в печи за счет процесса теплопереноса установится некоторое стационарный уровень нагрева в каждой части печи. Слева (x = 0, см. рис.4.1) нагрев будет наибольшим, а справа (x = L) – наименьшим. Предположим, мы имеем датчик с прибором, который позволяет измерять температуру (термопара), будем вносить этот датчик в различные зоны печи, расположенные на заданном расстоянии x от левого края печи (x = 0), и фиксировать показания температуры. По мере продвижения к значению x = L показания будут уменьшаться, точки на графике будут располагаться все ниже. Какую температуру мы измеряем? Измерения относятся к той точке x, в которую помещена термопара, значит ли это, что мы измеряем температуру в точке? Надо учесть, что сама термопара имеет некоторый размер δx , который много меньше длины всего нагревательного устройства. Поэтому мы условно говорим, что измерение производится в «точке». Однако сам спай термопары, который и производит измерение температуры, не точечный, пусть δx = 1 мм.

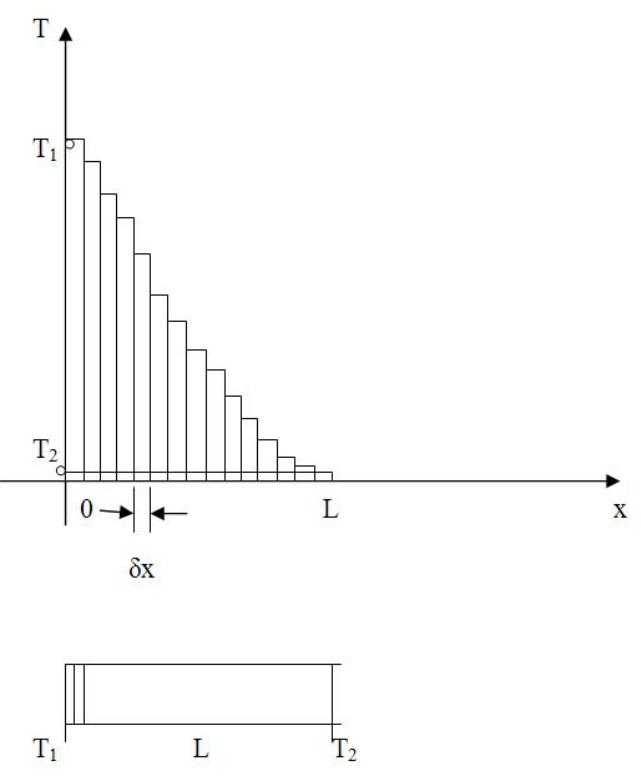
Рис.4.1. Измерение температуры в длинной трубчатой печи с неоднородным нагревом

Если размер L достаточно большой, скажем 1 м, то последовательное измерение температуры на каждом миллиметре длины печи позволяет построить плавную зависимость температуры от расстояния. Вместе с тем, каждая «точка» на этой зависимости имеет некоторый объем, т.е. ей соответствует определенный объем газа внутри печи. Сделаем оценку количества молекул в такой «точке», считая, что диаметр r = 1 см. Объем

V = δx × πr² ≈ 3×10^-7м³.

В таком объеме газа при нормальных условиях содержится 8∙10¹⁸ молекул.

Рассматриваемая неравновесная система состоит из большого количества «физических точек», каждая из которых достаточно велика, чтобы ее можно было рассматривать, как отдельную сложную систему. Для построения зависимости температуры от координаты, которая является описанием неравновесной системы, нам потребовалось провести реальные измерения с максимально возможной для нашего метода точностью. Сам факт измерения температуры в «физической точке» опирается на предположение, что внутри этой точки температура меняется настолько мало, что ее можно считать постоянной. Тогда «физические точки» неравновесной системы можно считать самостоятельными термодинамическими системами и применять к ним все законы «нормальной» равновесной термодинамики.

Таким образом, можно сформулировать некоторый принцип, позволяющий использовать законы «нормальной» термодинамики для неравновесных систем. Это принцип локального равновесия: любая неравновесная макроскопическая система может быть разбита на части, малые по сравнению с самой этой системой, но содержащие очень большое количество частиц (элементов); каждая из малых частей системы в любой момент времени находится в состоянии равновесия и характеризуется температурой, давлением, энтропией.

К разбиению на малые части в соответствии с принципом локального равновесия предъявляются следующие требования: части должны быть малыми, т.е. δx << L – это требование позволяет использовать методы математического анализа при описании процессов в неравновесной системе, состоящей из «физических точек»; части должны содержать большое количество частиц, т.е. δx >> d, где d – межатомное (межмолекулярное) расстояние – это требование предполагает возможность описания процессов в «физической точке» с помощью термодинамических законов (термодинамические законы пригодны для сложных систем, состоящих из большого числа элементов).

Есть еще одно требование, которое содержится в принципе локального равновесия. Оно связано с возможностью изменения параметров неравновесной системы не только в пространстве, но и во времени: время релаксации (время восстановления равновесного состояния) в «физической точке» t_рел (малой части системы, которая должна в любое момент времени находится в равновесии) должно быть намного меньше характеристического времени изменения внешних параметров τ, т.е. t_рел << τ.

Оценки применимости принципа локального равновесия показывают, что он пригоден почти для всех задач, которые возникают при анализе неравновесных систем и процессов. Его можно использовать для областей II и III диаграммы Бокштейна без ограничения, в некоторых случаях и для области IV.

Принцип локального равновесия позволяет локально использовать для описания неравновесных систем уравнения классической термодинамики. Как это осуществляется?

Во-первых, вместо термодинамических параметров для всей системы вводятся плотности этих параметров, т.е. значения параметров в единице объема системы (в «физической точке»). Осуществляется следующий переход:

Внутренняя энергия U [Дж] → плотность внутренней энергии u [Дж/м³]

Энтальпия H [Дж] → плотность энтальпии h [Дж/м³]

Энергия Гиббса G [Дж] → плотность энергии Гиббса g [Дж/м³]

Энтропия S [Дж/К] → плотность энтропии s [Дж/м³К]

…..

Такой переход дает возможность записать основное уравнение термодинамики – уравнение Гиббса, объединяющее 1-ое и 2-е начала термодинамики – для неравновесной системы через плотности термодинамических параметров

Tds = du + pdʊ - ∑ μ_i dc_i , (4.1)

где ʊ = (δx)³ – объем «физической точки», элемента системы, μ_i, c_i – химический потенциал и концентрация i – го компонента системы в данной точке.

Для неравновесной системы все величины, входящие в уравнение Гиббса в заданный момент времени являются функциями координат. Поэтому, во-вторых, для нахождения значения какой-либо экстенсивной термодинамической величины для всей системы надо просуммировать ее значения по всему объему системы - V. Например, энтальпия системы H равна

(4.2)

В-третьих, термодинамические параметры в неравновесных системах зависят не только от координат, но и от времени. Чтобы учесть при анализе неравновесных процессов эту зависимость, необходимо использовать величины, которые имеют размерности скоростей изменения параметров. Эти величины в физике известны, это потоки, в частности, потоки энергии I_Q, имеющие размерность Дж/м²с, и потоки вещества I_i (поток i – го компонента), с размерностью кг/м²с. Потоки, проходящие через неравновесную систему, носят название термодинамических потоков. Причины, вызывающие возникновение потоков, называют термодинамическими силами и обозначают X_j, где индекс j указывает, что данная термодинамическая сила является причиной возникновения j – го потока.

В-четвертых, учет сохранения энергии и вещества в неравновесной системе должен включать в себя зависимости плотности энергии и плотности (концентрации c_i) вещества для каждого компонента от координат и времени. Этой цели служат балансовые уравнения, которые называются уравнениями непрерывности. Для частных случаев распространения тепловой энергии и вещества i-го компонента уравнения непрерывности имеют вид

(4.3)

. (4.4)

Данная форма записи уравнений непрерывности соответствует отсутствию источников энергии и вещества в данной системе.