3. Отклонения от равновесия – термодинамический подход

Рассмотрим некоторую произвольную сложную систему, которая находится в состоянии термодинамического равновесия. Любые изменения в системе, в том числе эволюция, приводящая к появлению упорядоченных структур, могут происходить только при условии, что она находится в неравновесном состоянии, так как состояние равновесия является устойчивым и конечным в ряду последовательных состояний системы. Поэтому выведем систему из состояния равновесия и проследим за ее дальнейшим поведением (эволюцией), которое, что вполне естественно, будет зависеть от величины отклонения. При описании системы с помощью совокупности произвольных макроскопических параметров a_i ее состояние с разной степенью отклонения от положения равновесия - δa_i - можно представить с помощью схемы, которая носит по имени ее автора название диаграммы Бокштейна. Диаграмма Бокштейна представлена на рис. 3.1.

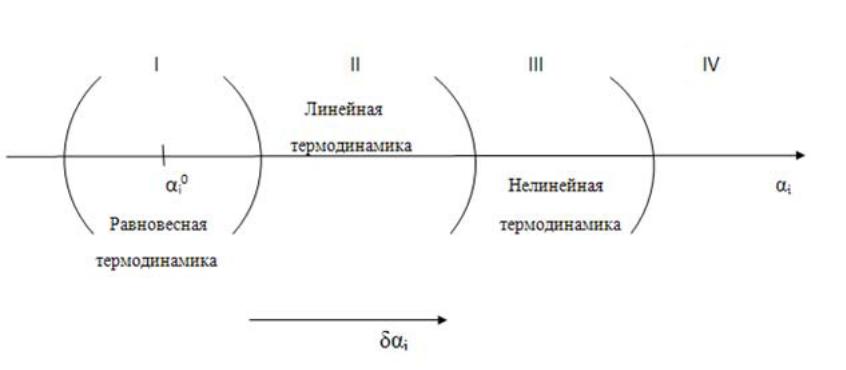
Рис.3.1. Диаграмма Бокштейна: термодинамические способы описания систем в зависимости от степени отклонения от равновесного состояния.

Степень отклонения от равновесия откладывается на диаграмме по горизонтальной оси, начало отсчета δa_i=0. Введем в качестве величины, которая, характеризует состояние системы, параметр A (это может быть температура, концентрация какого-либо компонента, фазовый состав и др.), который зависит от совокупности параметров a_i

A = A(a_i) (3.1)

Если δa_i = (a_i – a_i⁰) << a_i , то А вблизи равновесного состояния можно разложить в ряд Тейлора

, (3.2)

где А₀ – значение параметра в равновесии, А_i , A_ik – постоянные коэффициенты разложения.

Если δa_i очень мало, можно ограничиться значением А₀ и отбросить все остальные члены ряда. Этому состоянию соответствует область I на диаграмме. Область I может рассматриваться, как сферу применения равновесной термодинамики в качестве описания исследуемых систем.

Если δa_i мало, но не настолько, чтобы можно было пренебрегать возмущениями первого порядка, то функцию A(a_i) следует представить в следующем виде

, (3.3)

который демонстрирует линейную связь параметра системы с величиной отклонения от равновесия. Следовательно, процессы в этой области – обозначим ее как «область II» - могут быть проанализированы с помощью линейных законов. К этой области относятся процессы, которые описываются с помощью линейной термодинамики (о ней еще пойдет речь, поэтому здесь мы не расшифровываем этот термин).

Дальнейший учет членов разложения в случаях, когда отклонения от равновесия еще больше, приводят к появлению нелинейных членов типа Aδa_iδa_k и т.д. в зависимости A(a_i) (область III). Это значит, что в данной области на описание процессов не распространяется принцип суперпозиции – сумма действий различных причин (влияния различных параметров) не пропорциональна сумме их вкладов. В этом случае для описания процессов в неравновесных системах используют принципы нелинейной термодинамики неравновесных процессов.

При дальнейшем росте δa_i , когда перестает выполняться неравенство δa _i<< a_i , невозможно представить величину А в виде сходящегося ряда. Отклонения от равновесия настолько велики, и процессы происходят настолько интенсивно, что величину параметра А (т.е. измеряемую величину любого параметра), характеризующую всю систему в целом или ее отдельную часть (элемент), невозможно описать однозначно (область IV). Рассмотрение процессов в этой области с точки зрения термодинамики встречается со значительными сложностями. Однако современные методы анализа нелинейных математических моделей позволяют решать отдельные задачи и в этой далекой от равновесия области.

Подобное разграничение процессов в значительной степени условно – сама величина отклонения от равновесия, полагаемая для одних случаев малой, может оказаться значительной в других. Однако такой подход позволяет расставить принципы описания по мере их усложнения в соответствии с основным критерием – степенью отклонения от равновесия. Рассмотрим последовательно возможные способы применения термодинамического описания при увеличении величины этого критерия.