Критерии устойчивости. Функция Ляпунова.

Критерии устойчивости и функция Ляпунова используются в тех случаях, когда решить характеристическое уравнение не удается.

Приведем без доказательства критерий асимптотической устойчивости, который носит название критерия Гурвица.

Запишем характеристическое уравнение n – ой степени в следующем виде

(П.7)

Если коэффициенты C_i действительны, то все действительные части корней p_i отрицательны тогда и только тогда когда выполнены следующие условия:

1). С₁/С₀ > 0, C₂/С₀ > 0 … C_n/С₀ > 0;

2). Все главные миноры H_j квадратной матрицы

т.е. H₁ = C₁; H₂ = C₁C₂ – C₀C₃; … H_n = C_n H_n-1;

удовлетворяют неравенствам H₁ > 0; H₂ > 0;… H_n > 0.

Итак, если при исследовании стационарного состояния на устойчивость возникает характеристическое уравнение n – ой степени и для него выполняется критерий Гурвица, то стационарное состояние является устойчивым.

При исследовании устойчивости систем по траектории возможен анализ глобальной устойчивости (т.е. устойчивости во всей рассматриваемой области фазового пространства), который проводится с использованием потенциала, и локальной устойчивости (т.е. устойчивости вблизи особых точек).

Для не градиентных систем можно провести анализ глобальной устойчивости. Это было сделано Ляпуновым, он определил некоторую функцию V_L(q), заменяющую потенциал для не градиентных систем.

Определение функции V_L(q), функции Ляпунова.

1. V_L(q) и ее первые производные непрерывны в некоторой окрестности начала координат (особая точка взята в начале координат);

2. V_L(0) = 0;

3. Для в окрестности ;

4. - вектор состояния системы, значит и , поэтому , т.е. требование 4. означает, что

Введя функцию указанным способом Ляпунов доказал следующую теорему, которая является критерием глобальной устойчивости: «Если в некоторой окрестности особой точки существует функция Ляпунова , то особая точка устойчива; асимптотическая устойчивость имеет место в случае ».

Пример функции Ляпунова для двумерной системы приведен на рис. П.1.

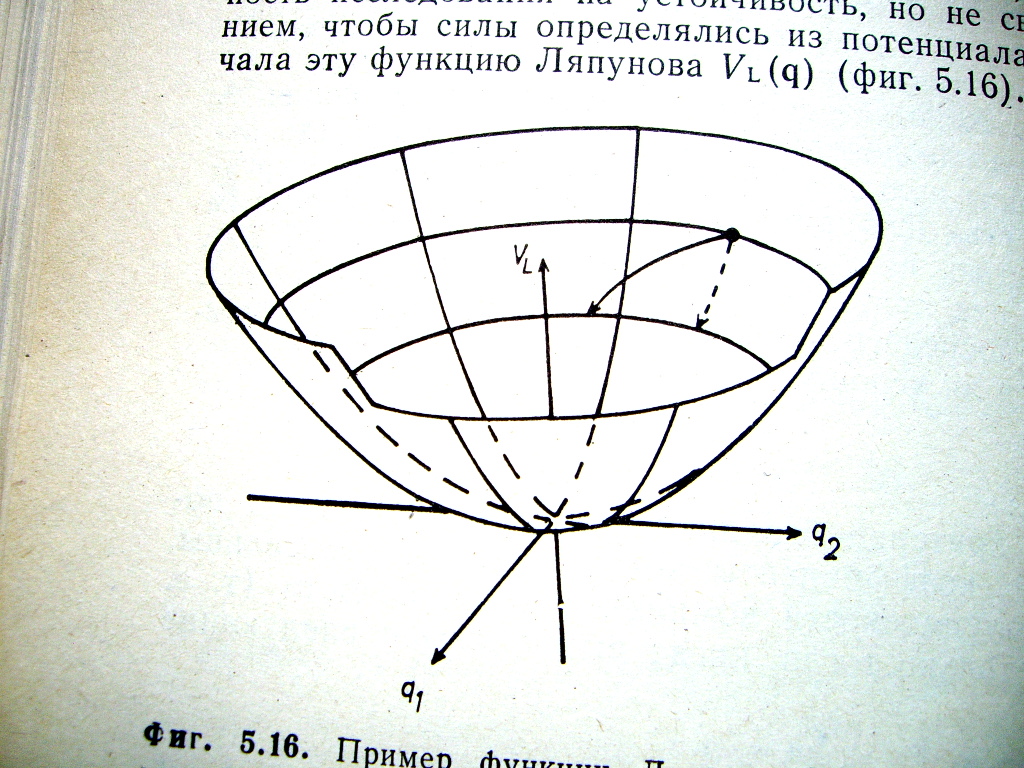
Рис.П.1. Общий вид функции Ляпунова

Данная поверхность внешне похожа на потенциальную. Отличие состоит в то, что при движении системы (шарика) по потенциальной поверхности (аналогу механического потенциала) система скатывается вниз всегда по траектории максимального наклона. Если существует функция Ляпунова, то в соответствии с условием 4. система также движется «вниз», но уже по любой траектории. Если , то траектория параллельна плоскости q₁ – q₂ - это случай не асимптотической маргинальной устойчивости.

Из критерия Ляпунова вытекает важное следствие: потенциал, если он существует, всегда является функцией Ляпунова.

132