11.2. Возбудимые среды

Среды, в которых возможно распространение одиночных волн, называются возбудимыми.

Рассмотрим вновь ячейку горения. Предположим, что в ней присутствует ингибитор, т.е. вещество, ухудшающее условия горения. Тогда тепловой эффект горения будет зависеть не только от температуры Т, но и от концентрации ингибитора - c_in (чем больше c_in , тем меньше Q). В этом случае имеем следующую модель процесса горения:

, (11.15)

а модель среды

. (11.16)

Если концентрация ингибитора не меняется в процессе горения, т.е. c_in играет роль внешнего параметра, среда остается бистабильной. При малых значениях c_in и Т > T₁ (см. рис.11.4) в среде распространяется волна зажигания; при тех же условиях, если c_in велико, в среде распространяется волна гашения.

Иначе среда реагирует на внешнее воздействие, если ингибитор выделяется в процессе горения, а затем уходит в окружающую среду. Зададим скорость изменения концентрации ингибитора без учета его диффузии в виде

, (11.17)

где – характеристическое время релаксации, которое велико по сравнению с временем перехода от холодного состояния к горячему; - равновесная концентрация ингибитора для данной температуры, монотонно растет с ростом Т.

Уравнение для ингибитора вместе с моделью среды описывает одиночную волну (уединенный бегущий импульс см. рис.11.4).

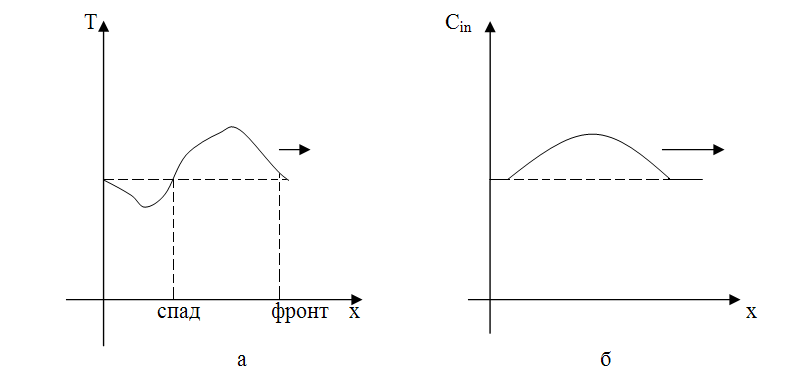
Рис.11.4. Распространение волны в возбудимой среде: а – изменение температуры в волне; б – изменение концентрации ингибитора в волне

Действительно, при загорании происходит резкий рост температуры – это фронт импульса, волна загорания. Затем происходит постепенное накопление ингибитора, и температура снижается, пока не опустится до предельного значения, при котором еще возможно горение: Т = Т₂ . Тогда наступает резкий спад температуры – волна гашения – и состояние среды возвращается к исходному. Концентрация ингибитора меняется плавно, без скачков, что является следствием большого времени релаксации – .

Библиографический список

1. Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. – М.: Мир, 2009. – 461 с.

2. Хакен Г. Синергетика. – М.: Мир, 1980. – 404 с.

3. Эбелинг В. Образование структур при необратимых процессах. – М.: Мир, 1979. – 279 с.

4. Жуховицкий А.А., Шварцман Л.А. Физическая химия. – М.: Металлургия, 2000. – 688 с.

5. Бокштейн Б.С. Диффузия в металлах. – М.: Металлургия, 1978. – 248 с.

6. Гилмор Р. Прикладная теория катастроф. Кн.1. – М.: Мир, 1984. – 350 с.

7. Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. – М.: Наука, 1990. – 272 с.

8. Петелин А.Л. Основы синергетики для металлургов: Курс лекций. – М.: МИСиС, 1993. – 118 с.

Приложение Дополнительные темы: Устойчивость систем с n переменными. Критерии устойчивости. Функция Ляпунова.

Обобщим результаты, полученные для систем с одной и двумя переменными на системы с произвольным количеством переменных.

Снова запишем динамические уравнения

. (П.1)

Так же, как и раньше, определим стационарные значения q_j^(s) из уравнений

F_j(q₁,q₂,...q_n) = 0. (П.2)

Далее по установленной схеме придадим каждой из переменных возмущения , подставим их в динамические уравнения, разложим динамические функции в ряд вблизи выбранной особой точки и оставим только линейные члены ряда. Получим систему из n обыкновенных дифференциальных уравнений, которую в сокращенной матричной форме можно записать в следующем виде

, (П.3)

где

Решение этой системы имеет вид:

. (П.4)

Для нахождения p₁ – p_n запишем характеристическое уравнение этой системы

, (П.5)

или

(П. 6)

Полученное алгебраическое уравнение n – ой степени в некоторых частных случаях (приведенное кубическое, биквадратное и т.д.) можно решить, найдя значения всех n корней. Однако общие выводы относительно устойчивости системы можно сделать не решая данного уравнения. Они заключаются в следующем:

- если действительные части всех (!) корней p_i меньше нуля – Re p_i < 0, то отклонения со временем затухают, т.е. соответствующая особая точка (стационарное состояние) устойчива;

- если хотя бы один из корней имеет Re p_i > 0 , то все возмущения будут со временем неограниченно возрастать, особая точка неустойчива;

- если некоторые из корней имеют нулевую действительную часть, то система совершает периодические движения вблизи особой точки с неизменной амплитудой – это маргинальная устойчивость, аналог не асимптотической устойчивости вблизи центра для систем с двумя переменными (иногда ее называют безразличной устойчивостью).