10.3. Катастрофа «сборка»

Пример 2. Задача с двумя управляющими параметрами.

Пусть потенциал системы имеет вид

, (10.4)

где a и b – управляющие параметры.

Построим стационарную поверхность в пространстве параметров q – a – b , для чего решим стационарное уравнение

. (10.5)

Внешний вид поверхности равновесия (стационарности), определяемый этим уравнением показан на рис. 10.3.

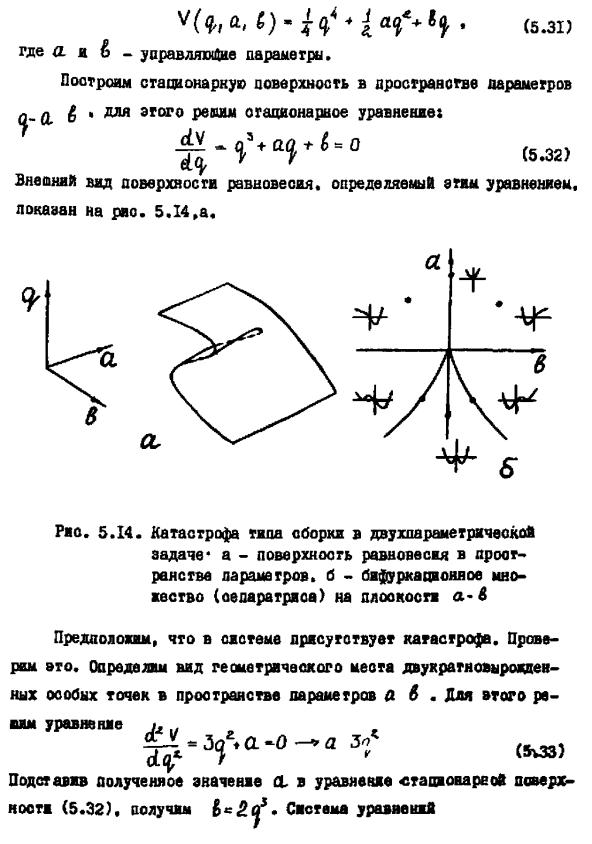
Рис.10.3. Катастрофа типа сборки в двухпараметрической задаче: а – поверхность равновесия в пространстве параметров; б – бифуркационное множество (сепаратриса) на плоскости a – b.

Предположим, что в системе присутствует катастрофа, Проверим это. Определим вид геометрического места двукратновырожденных особых точек в прастранстве параметров a – b. Для этого решим уравнение

. (10.6)

Подставив полученное значение а в уравнение стационарной (равновесной) поверхности, получим b = 2q² . Система уравнений

a = - 3q²

b = 2q³ (10.7)

определяет положение бифуркационного множества на плоскости управляющих параметров a – b. Это множество представляет собой линию, которая называется сепаратрисой, состоящую из двух симметрично расположенных ветвей, каждая из которых разделяет на плоскости параметров области с разным типом потенциала. Точка схода ветвей сепаратрисы носит название трехкратно-вырожденной особой точки. Ее положение (а она, как видно, находится в начале координат) определяется уравнением

, (10.8)

откуда q = 0 и a = b = 0.

Катастрофа канонической формы потенциала в данном примере также, видимо, из-за внешнего сходства поверхности равновесия с портновской сборкой, носит название катастрофы сборки.

Итак, если система градиентная, то с помощью теории катастроф можно исследовать структурную устойчивость системы, найти точки, линии или поверхности бифуркационного множества, а значит определить, где (при каких значениях управляющих параметров) расположена граница, разделяющая различные неравновесные фазы (состояния) системы. Для этого надо привести потенциал системы к каноническому виду и определить все n – кратновырожденные особые точки (n = 1,2…k, где k – общее количество параметров системы).

Несмотря на многообразие неравновесных процессов, на сложность реальных систем, предыдущее рассмотрение показало, что возможен некоторый единый подход, позволяющий в ряде случаев получить интересующие нас данные относительно поведения нелинейных систем. Этот подход можно попытаться выразить в виде краткого алгоритма, один из возможных вариантов которого мы приводим. Что надо сделать, чтобы исследовать поведение неравновесной нелинейной системы?

Необходимо построить динамическую модель исследуемой системы – представить динамику системы в виде дифференциальных уравнений, по возможности так, чтобы число независимых уравнений было не меньше числа независимых переменных (внутренних параметров).

Решая стационарные уравнения, нужно определить особые точки, которые соответствуют стационарным или равновесным состояниям.

Если модель описывается градиентной системой уравнений, исследовать устойчивость стационарных состояний по форме потенциала или путем линейного анализа устойчивости (можно использовать локальный критерий Гурвица, см. приложение 1); если полное число переменных не более пяти можно воспользоваться методами теории катастроф; для не градиентных систем следует использовать глобальный критерий Ляпунова (см. приложение).