10. Теория катастроф – взгляд со стороны
10.1. Катастрофы и анализ структурной устойчивости
Запишем динамическую модель произвольной системы в общем виде
,
(10.1)
где
- вектор состояния (внутренние параметры);
- управляющие параметры.
Исследуя
поведение системы мы, прежде всего,
определяли стационарные состояния
и тем или иным способом анализировали,
будет ли система оставаться в данном
стационарном состоянии или его покидает,
т.е. изучали устойчивость стационарных
состояний. Кроме того, мы говорили, что
при изменении одного или нескольких
управляющих параметров стационарное
состояние может терять устойчивость
(образование или разрушение диссипативных
структур, переход к турбулентности и
т.д.). Это означало, что происходит
неравновесный переход, система переходит
в другую фазу. С точки зрения динамической
модели это означает, что перестраивается
фазовый портрет системы, система теряет
структурную устойчивость – происходит
бифуркация. Вспомним, например
ангармонический осциллятор (или
соответствующие химические реакции).
Можно рассмотреть более сложные случаи, когда меняются сразу два (или более) управляющих параметра. Тогда задачу надо исследовать в пространстве двух управляющих параметров и одной переменной (внутреннего параметра), т.е. в 3-х мерном пространстве параметров. При этом вместо точки бифуркации появляется линия бифуркаций.
Поэтому задача определения структурной устойчивости в системах, содержащих несколько переменных и управляющих параметров, сильно усложняется и быстро теряет наглядность.
Исследование динамических моделей в пространстве внутренних и внешних параметров является предметом теории катастроф.
Катастрофами называются скачкообразные изменения, возникающие при внезапном ответе системы на плавные изменения внешних условий,. Катастрофами являются как равновесные фазовые превращения, так и неравновесные (динамические) фазовые переходы.
В теории катастроф исследуются только градиентные системы, общую модель которых можно схематически представить в виде уравнений
,
(10.2)
их стационарные (равновесные) состояния определяются условием
.
(10.3)
Французский
математик Р.Тома доказал теорему,
согласно которой для для общего числа
параметров (внутренних и управляющих)
k
5 потенциальная
функция системы
гладкой
заменой переменных может быть приведена
к некоторой канонической форме.
Разберем два примера исследования нарушений структурной устойчивости в простых системах, потенциал которых уже приведен к канонической форме.
10.2. Катастрофа «складка»
Пример 1. Рассмотрим систему с одним управляющим параметром. Пусть потенциал системы можно выразить в форме
,
(10.4)
где a – единственный управляющий параметр.
Такого типа потенциал мы имели в случае нелинейных химических систем. Форма потенциала при изменении параметра a меняется, как показано на рис.10.1.
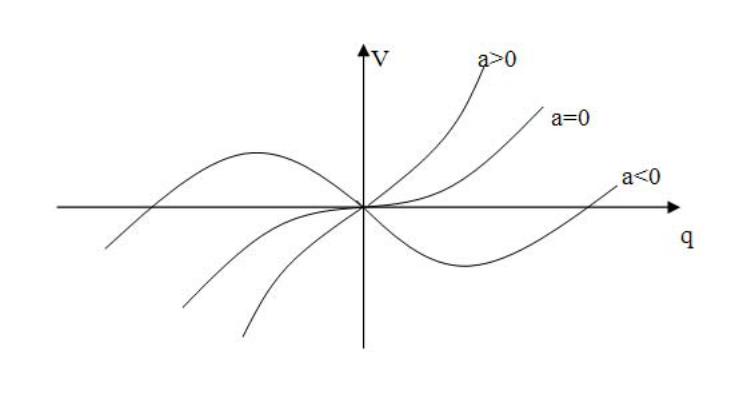
Рис.10.1. Задача с одним управляющим параметром в теории катастроф, форма потенциала
Определим, присутствует ли в этой системе катастрофа, т.е. скачкообразное изменение формы потенциала, и найдем вид бифуркационного множества.
Для этого определим геометрическое место точек стационарного состояния на плоскости параметров q – a . Если dV/dq = 0,то q2 + a = 0.
Полученное уравнение описывает геометрическое место особых бифуркационных (стационарных) точек (точек, соответствующих решению полученного уравнения). Уравнение имеет решение в отрицательной полуплоскости (см. рис.10.2). В правой положительной полуплоскости особых точек нет. Переход от отсутствия решений к двум решениям происходит, как видно, в точке a = 0, которую называют двукратно-вырожденной. Положение двукратно-вырожденной точки находят, решая уравнение d2V/dq2 = 0, из которого следует, что q = 0 и a = 0. Эта особая двукратно-вырожденная бифуркационная точка представляет собой искомое бифуркационное множество в пространстве управляющего параметра a (рис.10.2б). Таким образом, в системе имеет место катастрофа, которая называется катастрофой складки – по форме кривой стационарных состояний в плоскости параметров.
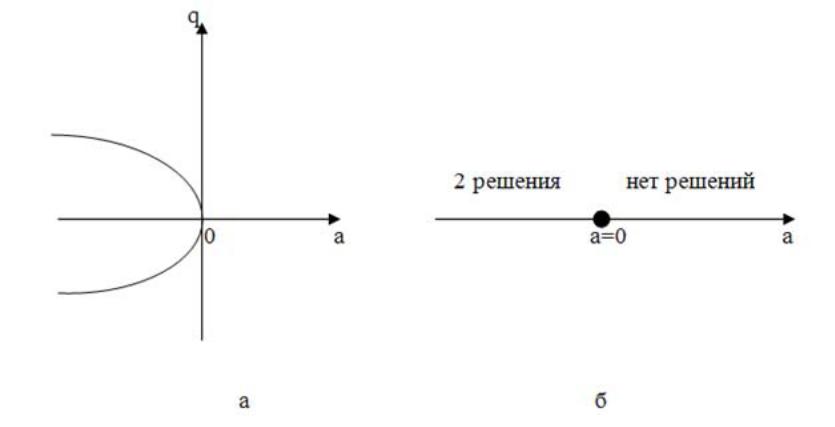
Рис.10.2. Катастрофа типа «складка»: а – геометрическое место особых (стационарных) точек; б – диаграмма решений и точка бифуркации.