9.2. Орбитальная устойчивость

Рассмотрим траекторию движения системы – u_j (t) – с точки зрения ее геометрической формы.

Пусть дана траектория u₁ (t); если для заданного > 0 найдется такое η > 0, что точка R, движущаяся по траектории, близкой к u₁ (t), (т.е. по «соседней» траектории в смысле близости начальных условий), в момент t₀ находится от u₁ (t) на расстоянии не более η и при t > t₀ остается на расстоянии не большем , то u₁ (t) – орбитально устойчивая траектория. Это означает, что, если при небольшом изменении переменных q_i системы в начальный момент времени ее траектория (орбита) не меняет свою форму в фазовом пространстве, то имеет место орбитальная устойчивость (рис.9.2).

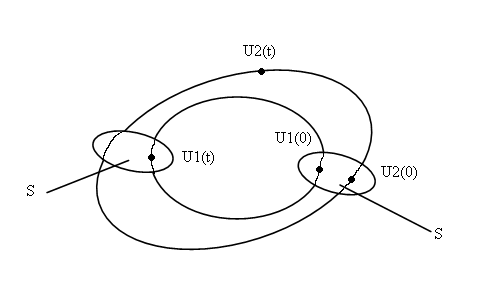
Рис.9.2. Движение систем при орбитальной устойчивости (соседние траектории)

Пример: два самолета, вылетевшие примерно в одно и то же время, но с разными скоростями, по одинаковому кольцевому маршруту, пролетают по орбитально устойчивой траектории для данной серии полетов. Это несмотря на то, что расстояние между самолетами в процессе полета все время увеличивается.

Орбитальная устойчивость также может быть асимптотической – в том случае, если расстояние между точкой R , движущейся по траектории, первоначально близкой к u₁ (t), и самой траекторией u₁ (t) стремится к нулю при t → ∞.

Еще один пример системы с двумя переменными, показывающий, в чем отличие орбитальной устойчивости от устойчивости по траектории. Рассмотрим движение материальной точки, которое в полярных координатах выражается уравнениями:

(9.3)

Это движения по окружностям, причем, чем больше радиус окружности r , тем больше угловая скорость . Значит две частицы, которые в начале движения были на соседних орбитах с близкими радиусами, со временем расходятся вследствие отличия их угловых скоростей. Устойчивости по траектории нет. Но форма орбиты при небольших изменениях начального значения r не меняется. Следовательно, орбитальная устойчивость имеется.

9.3. Структурная устойчивость

Пусть даны уравнения динамической модели системы

q_j = F_j , (9.4)

функции F_j часто зависят не только от переменных q_j , но и от внешних параметров , которые называются управляющими параметрами. При фиксированных значениях управляющих параметров поведение системы, описываемое траекториями в фазовом пространстве, однозначно зависит от начальных условий. Картина, изображающая поле траекторий в интересующей нас области фазового пространства для всех возможных начальных условий, называется фазовым портретом системы. Если при небольших изменениях управляющих параметров структура фазового портрета остается без изменений, то говорят, что система обладает структурной устойчивостью.

Система является структурно неустойчивой, если при небольших изменениях, хотя бы одного из параметров, в фазовом портрете происходят структурные изменения. Что это значит? Основные качественные изменения фазового портрета происходят при изменении характера особых точек – при ветвлении решений, т.е. при бифуркациях, которые соответствуют неравновесным фазовым переходам системы. Таким образом, следует отметить, что структурная устойчивость нарушается при неравновесных фазовых переходах, когда состояние системы становится чувствительным к флуктуациям внешних (управляющих) параметров.