9. Общие вопросы устойчивости нелинейных систем

Понятие устойчивости, которое мы до сих пор многократно упоминали, является центральным при исследовании сложных нелинейных систем. Мы называли стационарное состояние устойчивым, если система при неизменных внешних условиях находится в нем неограниченно долго. Зададимся вопросом, по отношению к чему проявляется устойчивость системы. Мы уже говорили, что в реальных условиях существуют случайные неконтролируемые возмущения – флуктуации. Если система находится в устойчивом состоянии, то флуктуации, например, начальных условий не отразятся на дальнейшем поведении системы, она все равно останется в этом состоянии. Наоборот, флуктуации, как бы они не были малы, помешают системе задержаться на вершине горы, в неустойчивом состоянии. Значит, мы говорим об устойчивости по отношению к флуктуациям.

Для проведения исследования системы, находящейся в заданном состоянии (стационарном или нестационарном), на устойчивость, необходимо математически определить понятие устойчивости.

Существует несколько видов устойчивости систем.

9.1. Устойчивость по траектории

Рассмотрим некоторую траекторию u_j (t) как движение системы в фазовом пространстве. Эта траектория устойчива, если другие траектории, которые в начальный момент времени t = t₀ были рядом с траекторией u_j (t), не удаляются со временем (рис. 9.1)

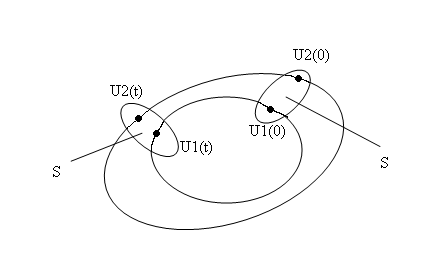
Рис.9.1. Поведение двух соседних траекторий движения системы в случае устойчивости по траектории

Поясним это обстоятельство. Каждая траектория – это единственный путь (поведение) системы при заданных начальных условиях. Разные начальные условия дают разные траектории в фазовом пространстве. Если мы говорим, что траектории были рядом в начальный момент времени, то это значит, что мы изучаем поведение системы при близких начальных условиях. Из того, что траектории со временем не расходятся (остаются поблизости друг от друга) следует, что значения переменных q_i , характеризующих систему, имеющие небольшое различие при близких начальных условиях, также незначительно отличаются друг от друга и во все последующие моменты времени. С математической точки зрения это означает, что, если задана окрестность S траектории u_j (t) в фазовом пространстве и если все соседние траектории, исходящие из этой окрестности, всегда остаются в этой окрестности, то траектория u_j (t) устойчива (см. рис.9.1). Если же нельзя найти такую окрестность, чтобы соседние траектории в любой последующий момент времени не покидали ее, то траектория u_j (t) неустойчива.

Можно сузить это определение. Пусть соседние траектории - u_j(t) и v_j(t) – обладают следующими свойствами

при t → ∞, (9.1)

это значит, что соседние траектории асимптотически стремятся друг к другу. Устойчивость, соответствующая данному определению называется асимптотической устойчивостью по траектории. Если же u_j (t)

при t → ∞, (9.2)

то мы имеем дело с асимптотически неустойчивой траекторией.