8.2. Предельные циклы

Проиллюстрируем особенности двумерных моделей неравновесных систем по-сравнению с одномерными на примере движения частицы (шарика) по дну круглого желоба с постоянной угловой скоростью ω. Запишем уравнения движения частицы в полярных координатах

q₁ = r cosφ;

q₂ = r sinφ, (8.13)

где r – радиус-вектор частицы, φ – полярный угол.

Они будут иметь следующую форму

= F(r);

φ = ω. (8.14)

Первое уравнение из (8.14) фактически задается формой желоба, а второе – отражает факт постоянства угловой скорости.

Пусть функция F(r) градиентная, т.е. можно ввести потенциал F(r) = – dV/dt. Тогда кривая V(r) при вращении вокруг оси (рис.8.7) образует поверхность, называемую потенциальной – «рельеф местности», в которой происходит движение частицы. Так как желоб имеет круговую форму, то и потенциальная кривая должна быть симметричной относительно оси вращения.

Рис.8.7. Потенциальная поверхность при движении частицы по кольцевому желобу.

Понятно, что какими бы ни были начальные координаты частицы r(0) и φ(0) , частица обязательно будет приближаться к стационарной круговой траектории, расположенной на самом дне желоба. Это происходит оттого, что желоб расположен между двумя склонами, наружным и внутренним, значит, частица при движении вдоль желоба всегда имеет минимальную потенциальную энергию.

На рис. 8.8 изображена фазовая плоскость q₁ – q₂ , на которой траектория движения частицы при любых начальных значениях координат будет иметь спиралеобразную форму.

Рис.8.8. Фазовый портрет движения частицы вблизи кольцевого желоба.

Если начальное значение радиус-вектора частицы меньше радиуса кругового желоба r₀, то траектория движения частицы будет представлять собой раскручивающуюся спираль, если же r(0) > r₀ – то скручивающуюся. В обоих случаях конечной будет круговая траектория по дну желоба. Замкнутая траектория, к которой стекаются все остальные траектории на фазовой плоскости, носит название устойчивого предельного цикла.

Возможен другой вариант функции F(r) (рис.8.9). В этом случае потенциальная кривая имеет более сложную форму, а потенциальная поверхность похожа на глубокую симметричную яму, по склону которой проходит неглубокий кольцевой желоб.

Рис.8.9. Устойчивый и неустойчивый предельные циклы.

Если начальный радиус-вектор частицы больше r₀, то частица скатится на дно желоба r = r₁ , дно желоба соответствует устойчивому предельному циклу (как в предыдущем примере). Но если частица в начале движения имеет координату 0 < r(0) < r₀, то она скатится на дно ямы. Траектория при r = r₀ характерна тем, что все соседние траектории от нее удаляются – или в сторону дна ямы, или в сторону кругового желоба при r = r₁. Замкнутая траектория, от которой все соседние удаляются, называется неустойчивым предельным циклом.

Наряду с особыми траекториями – предельными циклами – которые присущи моделям с двумя переменными, в них присутствуют и особые, соответствующие стационарным состояниям, критические точки. Так точка с координатой r = 0 в обоих рассмотренных примерах функций F(r) является особой. В первом случае особая точка неустойчива – вершина холма, во втором – устойчива – дно ямы.

Поведение системы, находящейся на предельном цикле – это колебательный процесс. Если речь идет об устойчивом предельном цикле, то амплитуда колебаний не уменьшается со временем. Система испытывает самоподдерживающиеся колебания – автоколебания. Если в начальный момент времени система находилась на неустойчивом предельном цикле, то частота и амплитуда колебаний со временем меняются.

Тип колебательного состояния (фазы) зависит от того, каким способом система попадает на предельный цикл. Возвращаясь к рис.8.7 и рис.8.9 можно заметить, что траектории частицы, приводящие на предельный цикл от состояния r = 0, в первом и втором случаях качественно отличаются. Для частицы, находящейся в условиях, соответствующих рис.8.7, колебания возникают самопроизвольно: частица, начиная движение в неустойчивой особой точке, сама со временем попадает в желоб. Чтобы возникло колебательное движение достаточно бесконечно малого возмущения (флуктуации). Самопроизвольное возбуждение автоколебаний носит название мягкого возбуждения (бытовой пример мягкого возбуждения – механические часы после того, как их завели). В случае, показанном на рис.8.9 для перевода частицы из равновесного положения (r = 0) на устойчивый предельный цикл (r = r₁) надо преодолеть потенциальный барьер при r = r₀, т.е. преодолеть пороговое значение потенциала V(r₀). Такой способ перевода системы в автоколебательную фазу называется жестким возбуждением. Реализация того или иного типа возбуждения зависит от вида потенциала V(r) или, что то же самое, от вида функции F(r).

Как могут происходить неравновесные динамические фазовые переходы в системах, фазовые портреты которых содержат предельные циклы? Будем плавно менять вид функции F(r) так, чтобы глубина желоба на склоне ямы стала уменьшаться. В какой-то момент точки r₀ и r₁ сольются в одну точку перегиба (рис.8.10). Произойдет аннигиляция

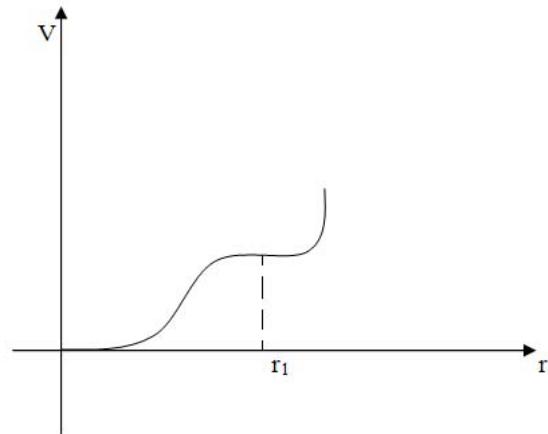
Рис.8.10. Слияние (аннигиляция) устойчивого и неустойчивого предельных циклов.

предельных циклов: устойчивого и неустойчивого, - которую можно представить бифуркационной схемой:

→ отсутствие предельного цикла

Итак, можно констатировать, что в двумерных динамических моделях, кроме особых точек, характеризующихся неизменностью во времени переменной (концентрации, координаты, численности популяции) и отвечающих стационарным состояниям системы, появляются особые траектории и соответствующие им бифуркации (неравновесные фазовые переходы).