7.5. Ангармонический осциллятор – нарушение временной симметрии

Пример 9. Разберем модель ангармонического осциллятора, которая описывается уравнением

(7.24)

Будем считать, что всегда k₁  0. Определим потенциал

(7.25)

Возможны два случая поведения системы:

k  0, тогда потенциал - это парабола в положительной полуплоскости, и состояние q = 0 будет состоянием устойчивого равновесия (рис.7.7а).

k  0 и тогда потенциал имеет вид, показанный на рис.7.7б, т.е. в системе при q₁ и q₂ появляются два равноценных состояния устойчивого равновесия, при q=0 ( вершина холма) - неустойчивое равновесие.

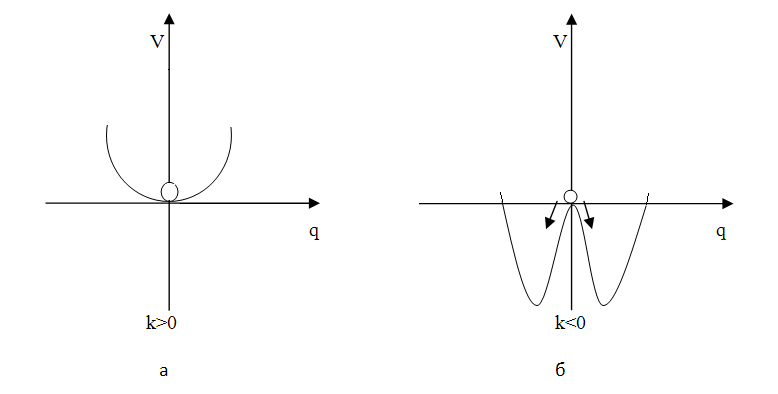
Рис.7.6. Потенциал для ангармонического осциллятора:а - k > 0; б - k < 0

Найти q₁ и q₂ можно, если приравнять dq/dt нулю и решить полученное алгебраическое уравнение. В результате

. (7.26)

Если построить зависимость равновесной координаты q_e от k (бифуркационную диаграмму), то она будет иметь вид вилки, показанный на рис.7.7: единственное в правой полуплоскости равновесное значение, равное нулю, при k = 0 раздваивается, и в левой полуплоскости имеются две ветви q_e, расходящиеся с ростом k. Разветвление решения, происходящее в бифуркационной точке при k = 0, можно проиллюстрировать схемой, которая называется бифуркационной схемой:

Рис.7.7. Зависимость равновесного значения переменной для ангармонического осциллятора от параметра k.

Что же происходит с системой при бифуркации. По мере приближения к нулю с положительной стороны, «склон» холма (см. рис.7.8а) становится все более пологим, шарик все медленнее скатывается в ямку. В точке k = 0 на рисунке имеет место нарушение симметрии в системе, т.е. шарик скатывается в одно из равновесных состояний. Симметрия нарушается не только в пространстве, но и во времени: шарик скатывается в одно из равновесных состояний необратимо. Нарушение временной симметрии происходит и в системе примера 7. Так, при С_А  С_А^кр стационарное состояние соответствует нулевой концентрации, реакция не идет. Это означает полную временную симметрию. При С_А  С_А^кр стационарное состояние существует при определенной концентрации, реакция идет в определенном направлении, симметрия отсутствует.

Приведенные примеры 7 и 8 показывают, что нарушение симметрии одной фазы и рождение симметрии другой фазы в точке перехода роднит неравновесные кинетические фазовые переходы с равновесными.

7.6. Эволюция систем – анализ динамической функции

Проведем изучение устойчивости динамических моделей систем с одной переменной. Динамическое уравнение таких систем имеет вид:

= F(q) (7.27)

Пусть система, описываемая данным уравнением, не градиентная. Поэтому для исследования ее будем анализировать характер устойчивости вблизи особых точек. Допустим, что графическое изображение функции F(q) в координатах F - q имеет вид, представленный на рис.7.8а. Чтоб определить значение q^(k), отвечающие стационарным состояниям, нужно решить уравнение F(q) = 0. Корнями такого уравнения являются q₀ = q^(k) при k = 1,2…n.

Рис.7.8. Графическое изображение системы с одной переменной

Для анализа устойчивости стационарных состояний дадим системе малое возмущение q:

q=q₀+ q q= q-q₀ . (7.28)

Разложим F(q) в ряд Тейлора вблизи точки q₀^(k):

(7.29)

Так как F(q₀) = 0, то в линейном приближении предыдущее уравнение можно переписать в виде

, (7.30)

где .

Решением уравнения будет

q(t)= q(0) e^pt (7.31)

Возможны две траектории движения системы вблизи особой точки:

- р0,

тогда при t  , стационарное состояние устойчиво;

- p  0,

тогда при t  , стационарное состояние неустойчиво.

Применим полученное решение к анализу ситуации, показанной на рис.7.8а. В точке q⁽¹⁾ p  0 ( вспомним что р = F^(q₀), так как наклон кривой в точке отрицателен, то отрицательна и производная). Значит стационарное состояние при q⁽¹⁾ устойчиво. Далее понятно, что в точке q⁽²⁾ p > 0, т.е. стационарное состояние при q⁽²⁾ неустойчиво. Сложнее обстоит дело с точкой q⁽³⁾ в ней р = 0. В этом случае для изучения устойчивости придется взять второй член разложения функции F(q). При этом получим уравнение

, (7.32)

решением которого будет

. (7.33)

Если q(0)  0 то система со временем возвращается в стационарное состояние при q⁽³⁾, но если q(0)  0, то она со временем от него уходит. Значит состояние при q⁽³⁾ неустойчивое.

Теперь, зная все обо всех стационарных состояниях заданной F(q), можно нарисовать фазовый портрет системы в фазовом пространстве, которое в случае одной переменной представляет собой ось q на рис.7.8б.

Таким образом, можно заключить, что при исследовании стационарных состояний систем с одной переменной возможны следующие случаи:

F(q₀^(k))  0 – стационарное состояние устойчиво,

F(q₀^(k))  0 – стационарное состояние неустойчиво,

F(q₀^(k)) = 0 – стационарное состояние неустойчиво.

Мы изучали устойчивость только для особых точек q₀. Во всех практически важных случаях этого оказывается достаточно, так как нас обычно интересует поведение системы не во всем фазовом пространстве, а в какой-то очень ограниченной его части. И в дальнейшем для большего числа переменных, мы сосредоточим внимание только на асимптотической устойчивости состояний.