7.2. Эволюция систем – метод потенциала

Будем считать, что модель градиентная и проанализируем ее с помощью потенциала. Введем понятие потенциала – функции V(q)

, (7.8)

В механике потенциал - это работа перемещения тела в поле силы F, взятая с обратным знаком. Понятие потенциала нам пригодится не только в механике. Следует учитывать, что его физическая трактовка не всегда будет столь наглядной, как в механике.

В данном разделе мы будем рассматривать только градиентные системы. Используем вначале понятие потенциала для анализа линейных механической и химической систем, а затем перейдем к нелинейным моделям.

Пример 1. Проанализируем с помощью потенциала состояние равновесия линейной механической системы - гармонического осциллятора . В соответствии с определением потенциал в данном случае запишется следующим образом .

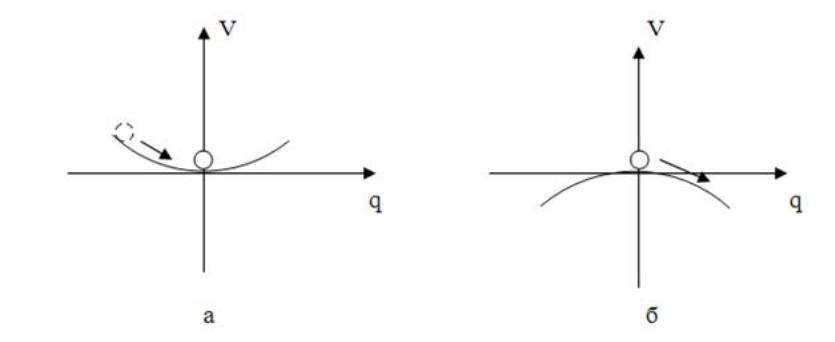
Рис.7.1. Механический потенциал гармонического осциллятора: а – k > 0; б - k < 0

Кривая потенциала представляет собой параболу, которая при k > 0 находится в положительной полуплоскости, а при к0 в отрицательной. Это представлено на рис.7.1. При k > 0 реализуется устойчивое состояние равновесия - система-шарик скатывается на дно оврага и остается там неограниченно долго.

При k  0 - неустойчивое состояние равновесия - шарик скатывается с вершины горы и уходит на бесконечность. При k = 0 происходит переход от устойчивого равновесия к неустойчивому (или наоборот). Графически зависимость равновесного значения координаты q_e от константы k, показана на рис.7.2. При k > 0 устойчивому равновесию соответствует нулевое значение координаты- q_e = 0 ( на рисунке в правой полуплоскости нулевое значение q_e выделено двумя сплошными линиями вблизи оси абсцисс). При k < 0 - равновесие неустойчивое (q_e по- прежнему равно нулю, но чтобы показать, что равновесие неустойчивое, на рисунке в левой полуплоскости оно выделено двумя пунктирными линиями).

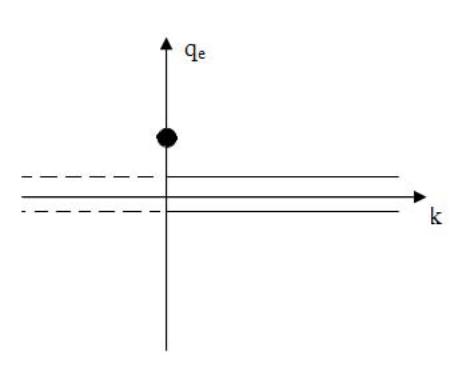
Рис.7.2. Диаграмма зависимости равновесных значений координаты от постоянного параметра k

Пример 2. Проанализируем протекание реакции разложения и производства компонента X (линейная система)

A ↔ X

Скорость изменения концентрации компонента Х - (dC_x/dt) - можно определить из кинетического уравнения

(7.9)

где С_А, С_х - концентрация веществ А и Х соответственно (и в дальнейшем нижний индекс при концентрации будет указывать, о каком веществе идет речь); Ф - приток компонента Х (химическая система открыта), k₁ и k_-1 – константы скоростей прямой и обратной реакций.

Если Ф постоянен, то стационарное состояние находим, приравняв dC_x/dt к нулю. Обозначив значение концентрации, соответствующее стационарному состоянию, через С₀ и решив стационарное кинетическое уравнение получим

(7.10)

Для исходного уравнения легко получить решение, которое будет выглядеть следующим образом

, (7.11)

где С_х(0)- концентрация компонента Х в начальный момент времени.

Как и для гармонического осциллятора для анализа данной реакции можно построить потенциал. Так как приведенное уравнение аналогично уравнению гармоничного осциллятора, то потенциал в этом случае будет иметь тот же вид. Отличие лишь в том что поскольку k_-1 всегда положительно, то случай, соответствующий рис.7.1б, не реализуется, а значит стационарное состояние С₀ будет всегда устойчивым.

Таким образом, исследование линейной системы - химической реакции - с помощью потенциала подтверждает вывод термодинамики линейных процессов: стационарное состояние в системе единственное и устойчивое.