21.Система уравнений Максвелла : диффер. Форма. Материальные уравнения.

Теорией Максвелла назвывается последовательная теория единого электромагнитного поля, создаваемого произвольной системой электрических зарядов и токов. В теории Максвелла решается основная задача электродинамики : по заданному распределению зарядов и токов отыскиваются характеристики создаваемых ими электрического и магнитного полей. Если мы из системы 4-х уравнений перейдем в проэкции на оси ( E - Ex Ey Ez, B - Bx By Bz), то не сможем решить ее, из-за большого кол-ва неизвестных. Для их нахождения пользуются так называемыми материальными уравнениями, характеризующими электрические и магнитные св-ва среды.

Анализ уравнений Максвелла.

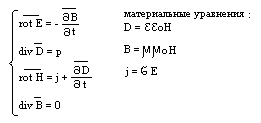1-е уравнение указывает на то, что поле является вихревым (вопр. 30). 2-е уравнение - Максвелл обобщил теорему Остроградского-Гаусса для электростатического поля. Он предположил, что она справедлива для любого электрического поля как стационарного, так и переменного. 3-е уравнение : См. ток смещения. В интегральной форме показывает, что циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур. 4-е уравнение - теорема Остроградского-Гаусса справедлива для любого магнитного поля.

Если электрические и магнитные поля стационарны (dD/dt = dB/dt = 0), то эти поля существуют независимо друг от друга. Электрическое поле описывается двумя уравнениями электростатики : rot E = 0 и div D = p, а магнитное поле - двумя уравнениями магнитостатики : rot H = j и div B = 0;

22-23. згас. колив. пружного маятника: ;

згасаючі колив. коливального контуру: ; ; коеф. згасання:  = L/2R; циклічна частота: .

24. вимушені коливання коливального контуру: ; враховуючи, що:  = L/2R та ₀ =1/LC: U = U_m  cos t; I_m = Q_m  ; де 25.складання колив.. одного напрямку і частоти: x₁ = A₁  cos (₁ + ₁) та x₂ = A₂  cos (₂ + ₂); A²(t) = A₁² + A₂² + 2A₁A₂  cos (₂ - ₁), а ;

биття - періодична зміна амплітуди при складанні колив. з близькими частотами: x = 2A  cos (  t/2)  cos t; T_м = 2/; T_б = 2/

складання  коливань: x / A = cos t; y / B = cos (t + ) = cos t  cos  - sin t  sin ; - траекторія точки, що здійснює еліптично поляризоване коливання, описує фігури Ліссажу.

29. пружні хв.:  = v  T; T = 1/; v =   ; /; р-ння пласкої біжучої хв.: S(x,t) = A  cos ( (t - x/v) + ₀); оскільки k =   v, то S(x,t) = A  cos (t - kx)

стояча хвиля - результат накладання зустрічних хвиль з однаковими частотами та амплітудами. Оскільки S₁ = A  cos (t - kx), S₂ = A  cos (t + kx), k = 2 /  та cos  + cos  = 2 cos (+)/2  cos (-)/2, то р-ння стоячої хвилі: S = 2A  cos kx  cos t

когерентні хвилі мають сталу у часі різницю фаз; інтерференція хвиль - накладання когерентних хвиль з постійним у часі розподілом амплітуд; max: k=2m; min: k=(2m+1); де =m - різниця ходу хвиль; k=2/