17

ЛЕКЦИЯ 11

Тема: АНАЛИЗ И СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ

1. Кинематический анализ кулачковых механизмов.

2. Синтез кулачковых механизмов

Кулачковым называется механизм, в составе которого кроме низших кинематических пар входят и высшие кинематические пары.

Кулачковые механизмы нашли широкое применение в технике (газораспределительные механизмы, командо-аппараты и т.д.) благодаря своей простоте (всего 2-3 звена) и возможностью выполнить практически любой закон движения.

1. Кинематическое исследование кулачковых механизмов

Рассмотрим несколько методов исследования кулачковых механизмов.

1.1. Исследование кулачковых механизмов методом замены высшей КП низшими парами

Вначале рассмотрим специальный кулачковый механизм, в котором звенья, связанные с элементами высшей КП представляют собой правильные круги (основной случай). Степень подвижности этого механизма

W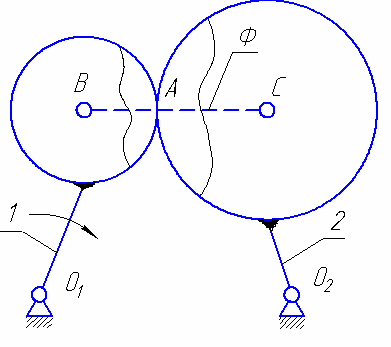 = 3_n - 2P₅ - P₄ = 3 · 2 - 2 · 2 - 1 = 1

Если двигать первое звено, второе также будет двигаться, но расстояние между центрами кругов В и С в любом случае будет постоянно. Следовательно, если образовать в точках В и С вращательные кинематические пары и соединить их звеном, то оно мешать движению не будет. Это условное звено обычно называют фиктивным звеном. Если выбросить части звеньев в окрестности КП А (на рисунке ограничено плавными тонкими линиями), то, с учетом фиктивного звена, движение первого и второго звена не изменится.

Что мы сделали? Мы образовали вращательные КП в центрах окружностей. Один элемент каждой пары соединили с фиктивным звеном, а второй элемент этих вращательных пар соединили со звеном, в центре кривизны которого образовали КП. Полученный механизм называется заменяющим.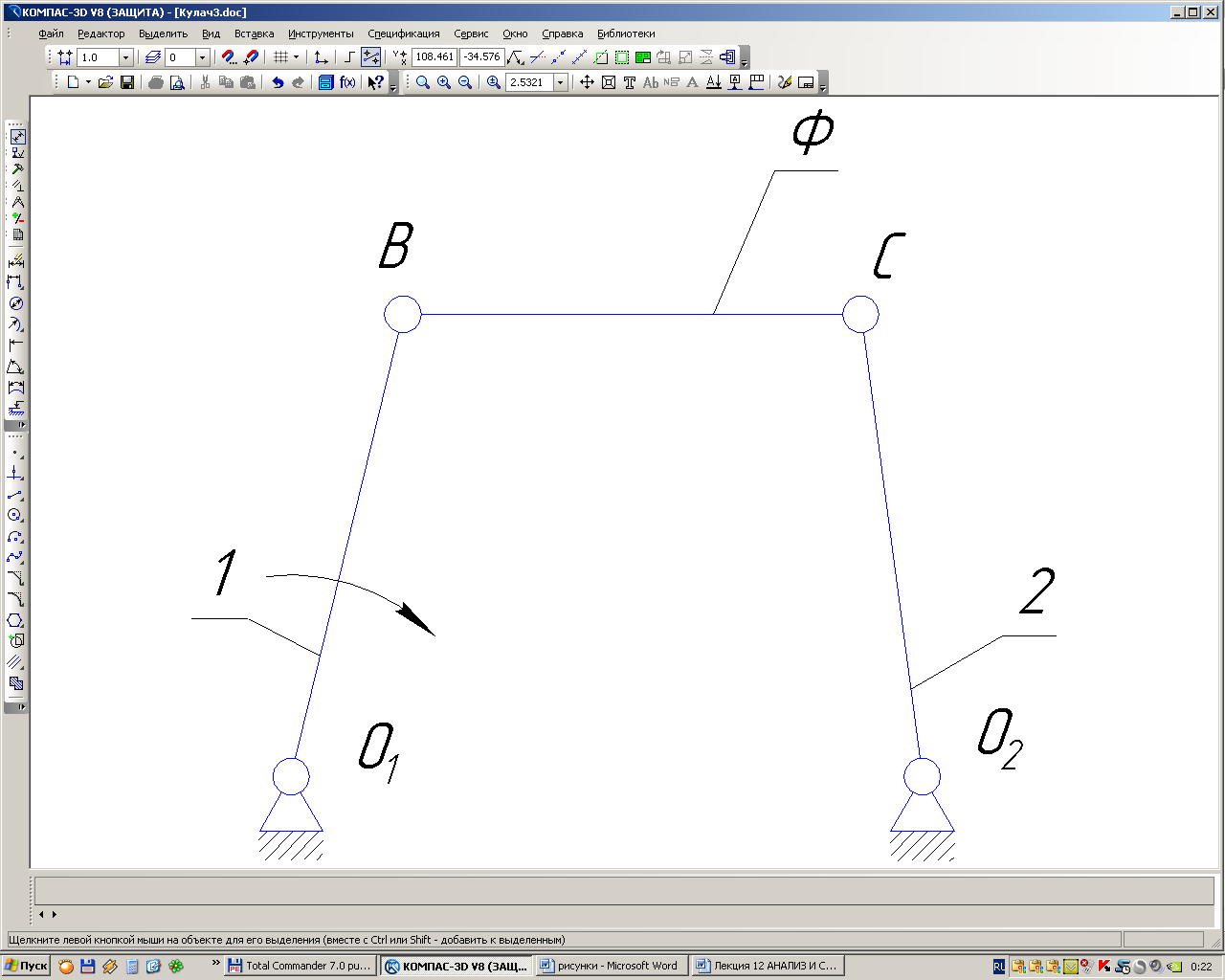

W = 3_n - 2P₅ - P₄ = 3 · 3 - 2 · 4 = 1

Его степень подвижности не изменилась и в кинематическом смысле он эквивалентен действительному механизму.

Рассмотрим механизм с произвольной высшей КП (общий случай).

Любую кривую в какой-то точке можно заменить другой кривой с разной степенью точности. Если касательной в точке, то ошибка будет первого порядка. Если кругом кривизны, то ошибка будет третьего и более высоких порядков малости. Следовательно, кривая окружности в точке касания эквивалентна самой кривой до производных второго порядка включительно. И этой ошибкой можно пренебречь.

Таким образом, заменяющий механизм будет эквивалентен в кинематическом смысле механизму с высшими парами до производных второго порядка включительно.

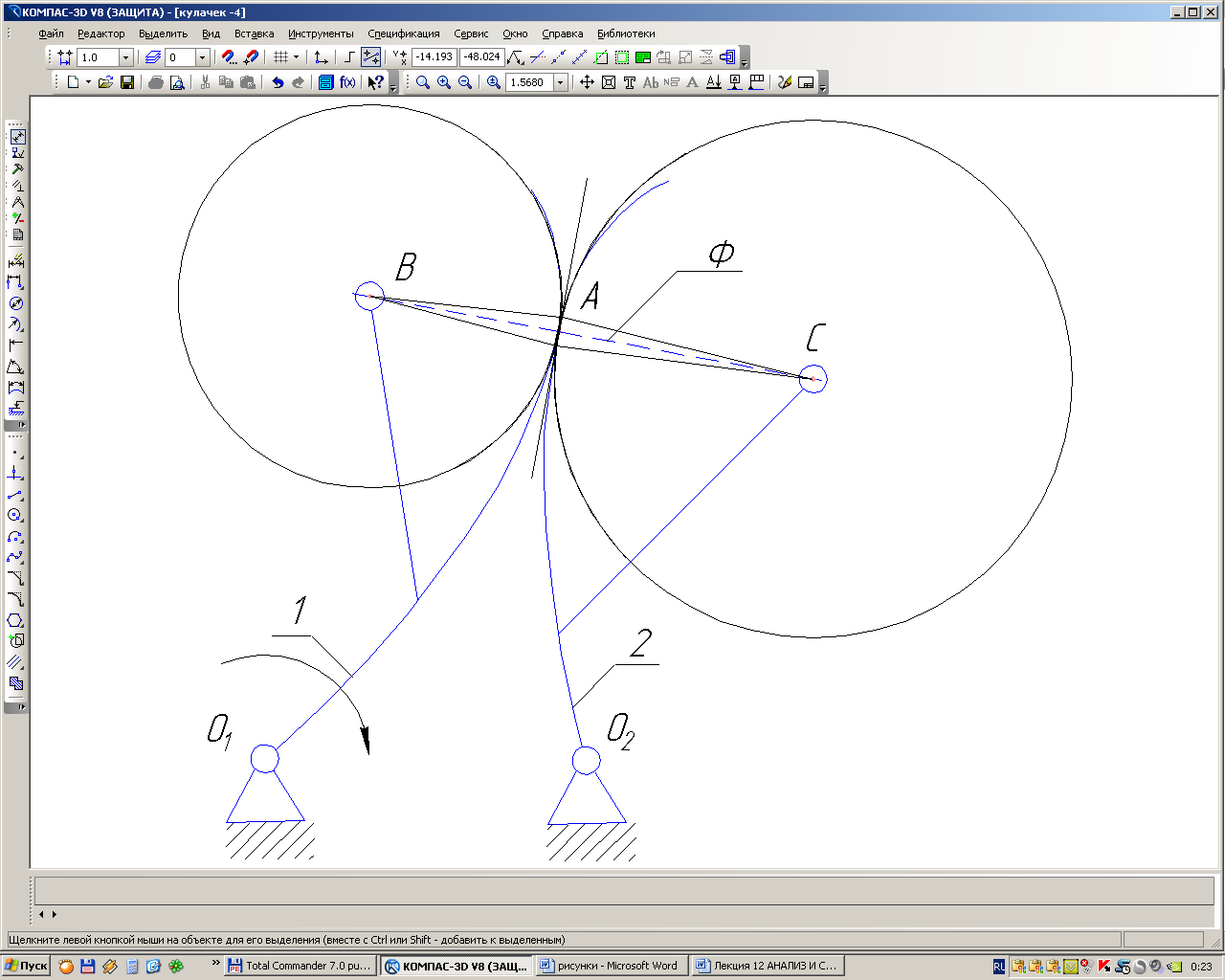
Как построить эти круги? Для этого необходимо найти центры кривизны звеньев в точке контакта любым методом (в данном случае определены методом хорд), которые и будут являться центрами кругов. Далее все делается, как и в основном случае.

П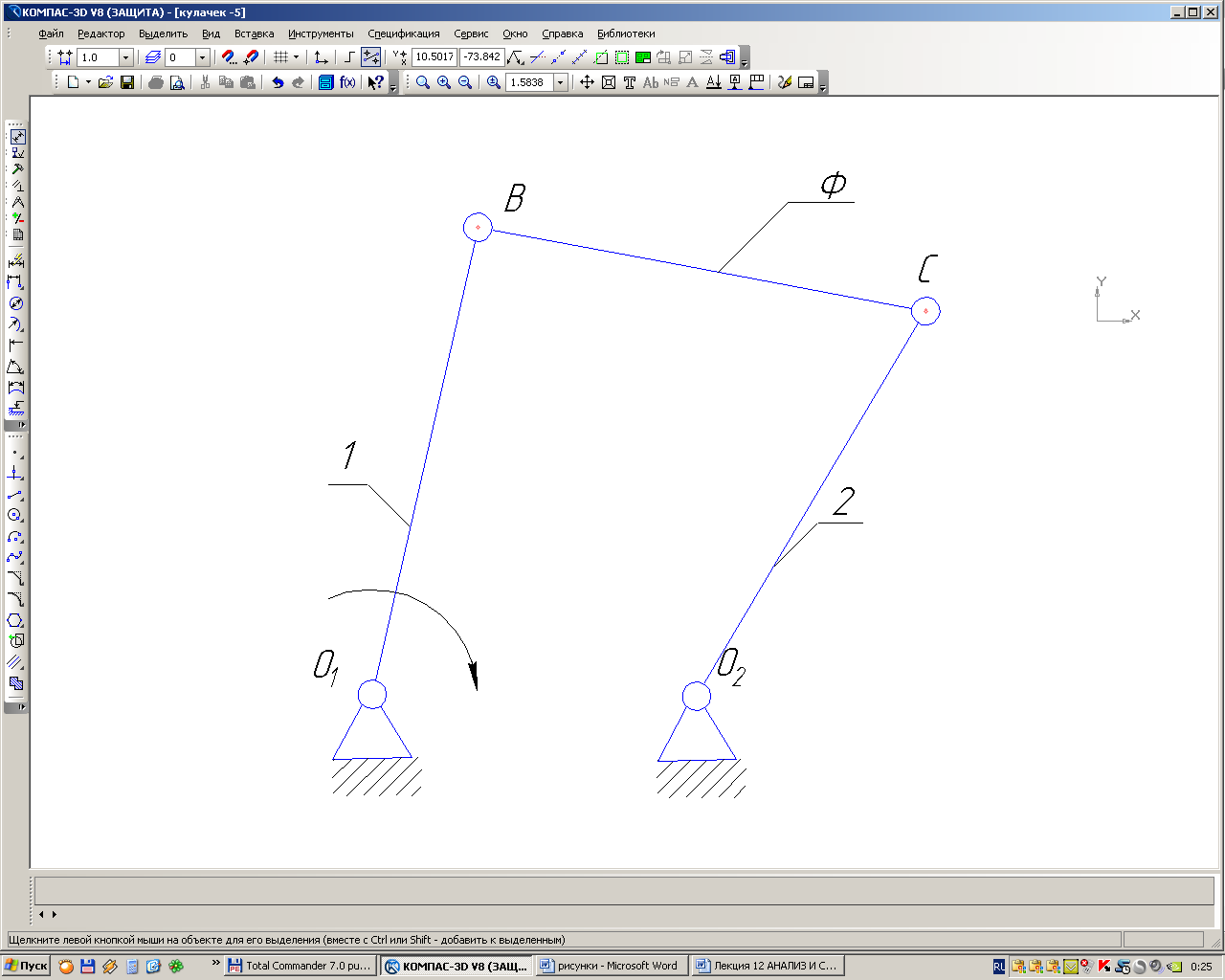 олученный заменяющий механизм будет эквивалентен только для данного положения действительного механизма, так как в общем случае длина фиктивного звена, как и первого и второго звена будут изменяться. Теперь можно проводить кинематическое исследование шарнирно-рычажного механизма известными методами.

Частные случаи замены высшей пары на низшие рассмотрены в литературе [1, 2, …].