Раздел 2. Транспортная задача п.2.1. Замкнутая и открытая модели тз

Пример 1. Решить транспортную задачу методом потенциалов.

bj ai	150	130	150	140
200	7	8	1	2
180	4	5	9	8
190	9	2	3	6

1. Проверим, является ли данная задача замкнутой.

Подсчитаем суммарные запасы груза и суммарные потребности заказчиков ,

.

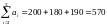Поскольку , модель транспортной задачи замкнутая, и задача имеет оптимальный план.

2. Построим первый опорный план транспортной задачи методом северо-западного угла.

Начинаем заполнение распределительной таблицы с верхней левой клетки, то есть построение исходного опорного плана начинаем с удовлетворения потребностей первого потребителя b₁ за счет запасов первого поставщика a₁. Для этого сравниваем запас a₁ = 200 с потребностями b₁ = 150. Так как a₁ > b₁, то потребности b₁ полностью удовлетворяем за счет a₁, и в первую клетку помещаем min (200, 150)=150. У первого поставщика осталось 50 единиц груза. Так как потребности первого получателя груза полностью удовлетворены, исключим из рассмотрения первый столбец, заполнив в нем оставшиеся клетки точками. Далее заполняем таблицу по строкам слева направо и сверху вниз. Следующая самая верхняя левая незаполненная клетка – (1,2). Потребителю b₂ поставляем 50 единиц груза, оставшихся у первого поставщика. Поскольку от первого поставщика весь груз вывезен, заполняем оставшиеся клетки первой строки точками. Второму получателю, пока что, недопоставлено 80 единиц груза. Следующая незаполненная клетка – (2,2). Потребителю b₂ отправляем недостающие 80 единиц груза, при этом его потребности полностью удовлетворены, поэтому оставшиеся клетки во втором столбце заполняем точками. У второго поставщика a₂ осталось еще 100 единиц груза. Аналогичным образом заполняем оставшиеся клетки, пока не удовлетворим всех потребителей и не вывезем все запасы груза у поставщиков.

bj ai	150	130	150	140
200	7 150	8 50	1 *	2 *
180	4 *	5 80	9 100	8 *
190	9 *	2 *	3 50	6 140

В результате распределения груза получим первый опорный план, в котором x₁₁ = 150, x₁₂ = 50, x₂₂ = 80, x₂₃ = 100, x₃₃ = 50, x₃₄ = 140. Эти переменные соответствуют заполненным клеткам и являются базисными, остальные переменные, соответствующие клеткам с точками, являются свободными (значения свободных переменных равны нулю). Первый опорный план можно представить в матричном виде

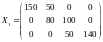
Число заполненных клеток k = 6. Это число должно равняться рангу системы ограничений r = m + n – 1 = 3 + 4 – 1 = 6. Так как k = r = 6, то построенный план является невырожденным. Подсчитаем затраты на перевозку по этому плану

.