
- •Численный расчет нестационарного теплового состояния лопатки авиационного гтд
- •Содержание:
- •Численный расчет нестационарного теплового состояния
- •1.1 Определение теплового состояния дефлекторной лопатки
- •1.1.1 Исходные данные для расчета дефлекторной лопатки.
- •Принятые обозначения и допущения
- •1.1.3 Краевая задача нестационарной теплопроводности, описывающая
- •Определение характерных температур
- •Расчет теплоотдачи от газа к лопатке
- •Расчет теплоотдачи от лопатки к охлаждающему воздуху
- •Результаты расчета
- •График зависимостей температуры стенки лопатки со стороны газа и охладителя от времени для одноконтурного двигателя
- •График зависимостей температуры стенки лопатки со стороны газа и охладителя от времени для двухконтурного двигателя
- •1.2 Исследование теплового состояния матричной лопатки соплового аппарата первой ступени турбины гтд методом конечных элементов
- •1.2.1 Постановка задачи исследования теплового состояния матричной лопатки.
- •Основные соотношения метода конечных элементов
- •Определение параметров теплоотдачи матричной лопатки гтд
- •Результаты расчета
- •Стационарное температурное поле в матричной лопатке
- •График зависимостей максимальной и минимальной температур матричной лопатки от времени
- •2 Расчет кольцевого теплообменника змеевикового типа.
- •2.1 Схема и описание воздухо-воздушного теплообменника гтд
- •Результаты расчета теплообменника
- •2.3. Поверочный расчета теплообменника
- •Список литературы
1.1 Определение теплового состояния дефлекторной лопатки
методом конечных разностей
1.1.1 Исходные данные для расчета дефлекторной лопатки.
Параметры рабочего цикла:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Исходные данные для расчета дефлекторной лопатки:
участок профиля – выходная кромка;
характерная скорость газа wг = 200 м/с;
характерная скорость охладителя wохл = 150 м/с;
характерный геометрический размер для охладителя l 0, охл, III = 2,0 мм;
характерный геометрический размер для газа l 0, г, III = 80 мм;
толщина стенки лопатки
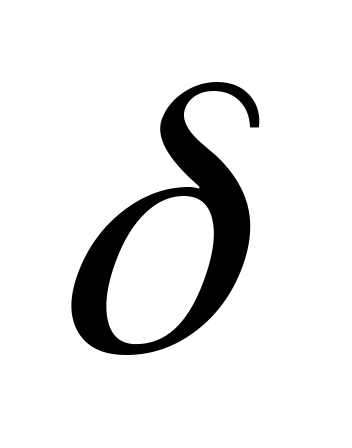 =2,0
мм;
=2,0
мм;материал лопатки ЖС6;
глубина охлаждения воздуха в теплообменнике
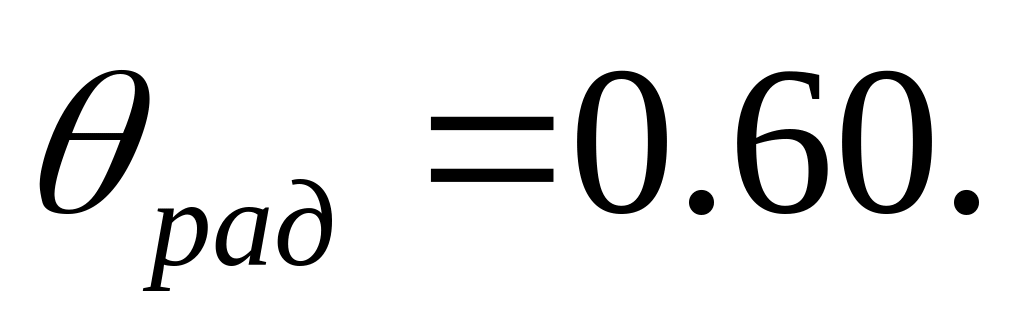
Принятые обозначения и допущения
Весь профиль дефлекторной лопатки условно разделяется на три участка: входная кромка I, средняя часть II (включающая как спинку, так и корытце) и выходная кромка III.
Для упрощения расчета сделаем следующие допущения:
перетоком тепла вдоль профиля и по высоте лопатки пренебрегаем;
температуру газа
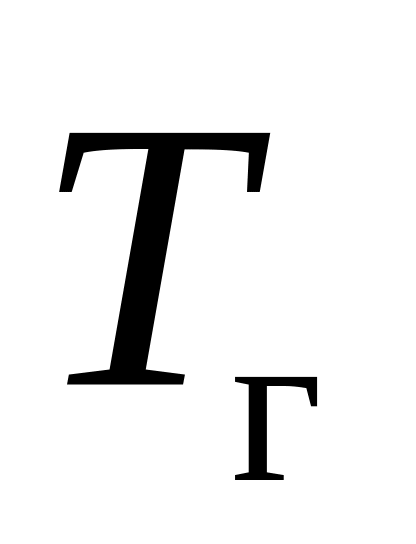 и температуру охлаждающего воздуха
и температуру охлаждающего воздуха
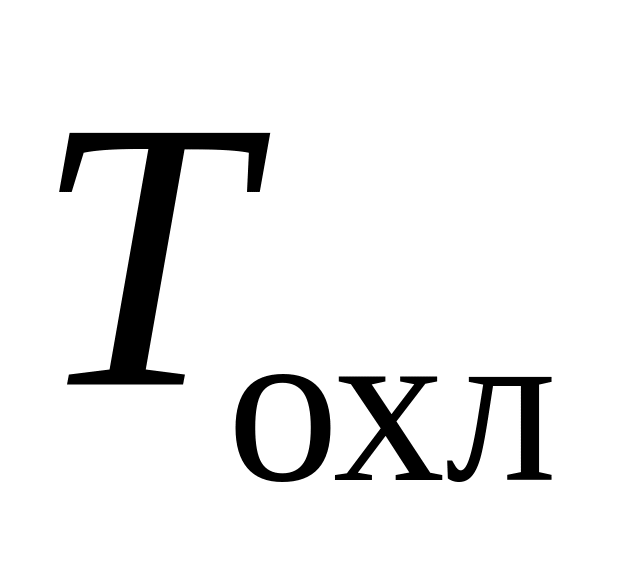 считаем постоянными и одинаковыми для
всего профиля поперечного сечения;
считаем постоянными и одинаковыми для
всего профиля поперечного сечения;коэффициенты теплоотдачи от газа к лопатке
 и от лопатки к охлаждающему воздуху
и от лопатки к охлаждающему воздуху
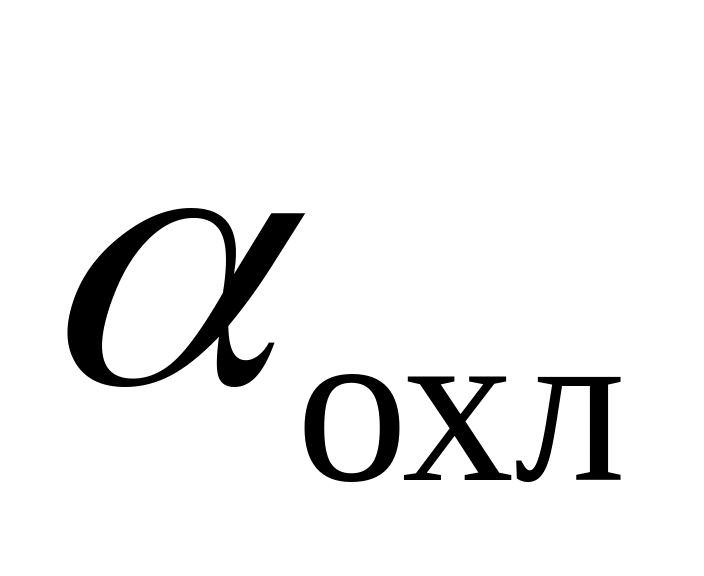 считаем постоянными по времени,
одинаковыми в пределах каждого участка
и равными их соответствующим средним
значениям на участке;
считаем постоянными по времени,
одинаковыми в пределах каждого участка
и равными их соответствующим средним
значениям на участке;
участок I входной кромки условно рассчитываем как полый цилиндр с наружным радиусом R и толщиной стенки d;
участки II и III со стороны спинки и корытца моделируем неограниченными пластинами постоянной толщины.
Следствием приведенных допущений является одномерность температурного поля на каждом участке, то есть изменение температуры происходит только в направлении нормали к обтекаемой поверхности.
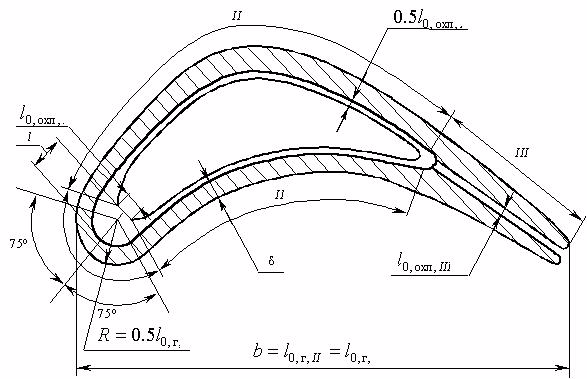
Рисунок 1 – Участки профиля дефлекторной лопатки
1.1.3 Краевая задача нестационарной теплопроводности, описывающая
тепловое состояние лопатки.
С учетом принятых допущений развитие во времени температурного поля на участках профиля лопатки описывается следующей краевой задачей нестационарной теплопроводности с граничными условиями третьего рода на ограничивающих поверхностях:
![]() (1.1)
(1.1)
![]() ;
(1.2)
;
(1.2)
![]() (1.3)
(1.3)
![]() ,
(1.4)
,
(1.4)
где
x
и
![]() - соответственно пространственная и
временная переменные,
- соответственно пространственная и
временная переменные,
![]() - искомая температура, T0
– начальная температура лопатки, Tw,охл
и Tw,г
– температуры поверхности лопатки со
стороны охлаждающего воздуха и
высокотемпературного газа соответственно,
- искомая температура, T0
– начальная температура лопатки, Tw,охл
и Tw,г
– температуры поверхности лопатки со
стороны охлаждающего воздуха и
высокотемпературного газа соответственно,
![]() - коэффициент геометрической формы. При
- коэффициент геометрической формы. При
![]() задача (1.1) – (1.4) описывает тепловое
состояние средней части профиля лопатки
и выходной кромки, и в этом случае
необходимо положить
задача (1.1) – (1.4) описывает тепловое
состояние средней части профиля лопатки
и выходной кромки, и в этом случае
необходимо положить
![]() ;
при
;
при
![]() приведённая
краевая задача описывает тепловое
состояние входной кромки лопатки, и
тогда
приведённая
краевая задача описывает тепловое
состояние входной кромки лопатки, и
тогда
![]()
![]() где
где
![]() внутренний
радиус входной кромки.
внутренний
радиус входной кромки.
1.1.4 Конечно-разностная схема
При численном решении краевой задачи теплопроводности температуру определяют в дискретных точках пространства и в дискретные моменты времени. Для задачи (1.1) – (1.4) неявная абсолютно устойчивая в счете безытерационная конечно-разностная схема имеет вид
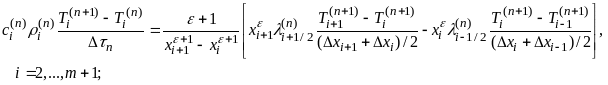 (1.5)
(1.5)
![]() (1.6)
(1.6)
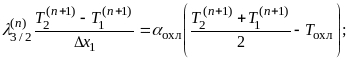 (1.7)
(1.7)
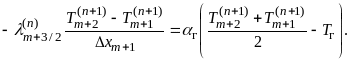 (1.8)
(1.8)
Здесь
предполагается, что геометрическая
область, в которой ищется решение задачи
(1.1) – (1.4), разбита на m
слоев таким образом, что вектор нормали
к границе каждого слоя коллинеарен
орт-вектору оси Ox (см. рисунок 2). Через
![]() и
и
![]() обозначены координаты соответственно
левой и правой границы i–го
слоя. С целью распространения
конечно-разностного уравнения (1.5) на
крайние (2-й и m+1-й)
слои области введены также два фиктивных
(1-й и m+2-й)
граничных слоя. Толщина каждого из
фиктивных слоёв принимается равной
толщине соответствующего прилегающего
к нему слоя области, то есть
обозначены координаты соответственно
левой и правой границы i–го
слоя. С целью распространения
конечно-разностного уравнения (1.5) на
крайние (2-й и m+1-й)
слои области введены также два фиктивных
(1-й и m+2-й)
граничных слоя. Толщина каждого из
фиктивных слоёв принимается равной
толщине соответствующего прилегающего
к нему слоя области, то есть
![]()
![]() Верхние индексы (n)
и (n+1)
обозначают два последовательных
временных слоя
Верхние индексы (n)
и (n+1)
обозначают два последовательных
временных слоя
![]() и
и
![]() разделённых промежутком времени
разделённых промежутком времени
![]()
Температуры
![]() (i
= 1, 2,…, m+2)
определяются в серединах соответствующих
пространственных слоев.
(i
= 1, 2,…, m+2)
определяются в серединах соответствующих
пространственных слоев.
Плотность, теплоемкость и коэффициент теплопроводности рассчитываются в (1.5) – (1.8) следующим образом:
![]()
![]()
Отметим, что температуры наружной и внутренней поверхностей лопатки явно не присутствуют в уравнениях (1.5) – (1.8). При необходимости, на n-м временном шаге они могут быть определены по формулам
![]() .
.
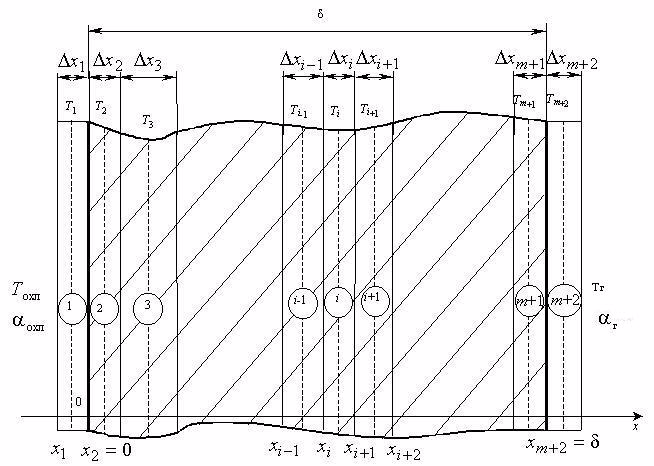
Рисунок 2 – Схема разбиения
