1.7 Технология проведения эксперимента

В данном исследовании мы будем проводить 4 эксперимента по взаимосвязи выбранных факторов. Проводя эксперимент №1, мы выбираем значение температуры 105°С и значение длительности копчения 2часа; в эксперименте №2 – значение температуры 155°С и времени 2 часа; в эксперименте №3 – 105°С и 4 часа; и в последнем 4-м эксперименте - 155°С при длительности 4 часа. Затем с помощью математических расчетов выявим, какой из проведенных экспериментов является наиболее оптимальным.

1.8 Результаты эксперимента

Составим матрицу результатов эксперимента, где указаны значения у’, y”, .

Таблица 2 –Полная матрица эксперимента

№ опыта	Значение фактора		Значение фактора				Результаты эксперимента
	ист.знач.	код.знач.	ист.знач.	код.знач.
1	105	_	2	_	+	+	107	111	109
2	155	+	2	_	+	_	149	153	151
3	105	_	4	+	+	_	114	126	120
4	155	+	4	+	+	+	152	164	158

= ;

2 Обработка результатов эксперимента

2.1 Определение ошибки повторных опытов по критерию Стьюдента(t)

Из таблицы 2 возьмем значение , , и вычислим среднее квадратичное отклонение, которое определяется по формуле:

,

где S – среднее квадратичное отклонение;

n – число параллельных опытов;

– значение эксперимента.

Сравним полученные значения ошибки с табличным значением критерия Стьюдента при 5 % уровне значимости (при числе степеней свободы f = n – 1) и если условие не выполняется, то результаты не считаются ошибочными и, следовательно, участвуют в дальнейших расчетах.

= 12.71

Т.к. 0,71<12,71 – оба результата участвуют в дальнейших расчетах.

Т.к. 0,71<12,71 – оба результата участвуют в дальнейших расчетах.

Т.к. 0,71<12,71 – оба результата участвуют в дальнейших расчетах.

Т.к. 0,71<12,71 – оба результата участвуют в дальнейших расчетах.

Таблица 3 – Матрица результатов эксперимента

N				Si	ty’	ty’’	Si2
1	107	111	109	2.83	0.71	0.71	8
2	149	153	151	2.83	0.71	0.71	8
3	114	126	120	8.49	0.71	0.71	72
4	152	164	158	8.49	0.71	0.71	72
							∑=160

2.2 Оценка дисперсии среднего арифметического в каждой строке матрицы

Из таблицы 3 возьмем значение , , и вычислим дисперсию отклонения, которая определяется по формуле:

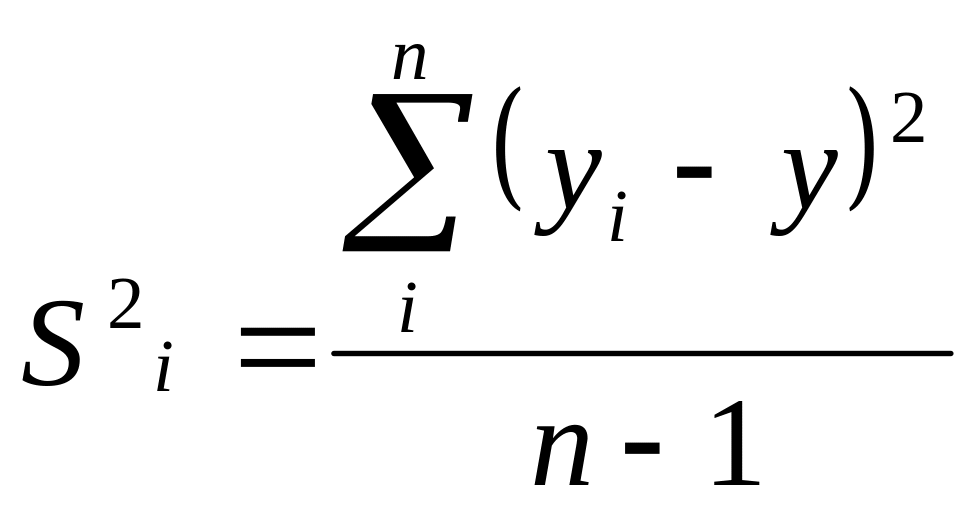
S²_i - дисперсия среднего арифметического

=8

=8

=72

=72

Дисперсия воспроизводимости (параметра оптимизации) (S²_{y}) рассчитывается по формуле:

Где: S²_{y} - дисперсия воспроизводимости;

N – число опытов в эксперименте;

Определение однородности дисперсии по критерию Кохена:

Табличное значение К=0.68, так как 0.45<0.68, значит, что дисперсия однородна.

Проверка однородности дисперсии по критерию Фишера:

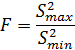
Табличное значение F=164, так как 9<164 дисперсия однородна.