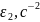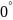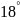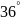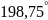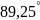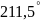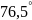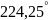- •Пояснительная записка
- •«Теория машин и механизмов»
- •Ведение
- •1. Структурный анализ механизма
- •3.2 Определение угловых скоростей звеньев механизма
- •4. Третья задача кинематического анализа
- •4.1 Определение ускорений всех точек и звеньев механизма
- •4.2 Определение угловых ускорений шатуна
- •5. Кинематические диаграммы
- •6. Кинетостатический анализ механизма
- •6.2 Расчет ведущего звена
- •7. Синтез кулачкового механизма
- •8 . Расчет параметров зубчатых колес
- •9 . Синтез планетарного редуктора
- •9.1 Подбор чисел зубьев методом сомножителей
- •9.2 Графический метод исследования планетарных передач
- •З аключение с писок используемых источников
4.2 Определение угловых ускорений шатуна
Находим значения угловых ускорений шатуна в каждом положении по формуле:
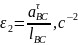
Числовые значения угловых ускорений приведены в таблице 7.
Угловые ускорения шатуна. Таблица 7
c^-2 № |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
42,92 |
63,776 |
42,923 |
0 |
42,923 |
63,776 |
42,92 |
5. Кинематические диаграммы
Построим диаграммы перемещения, скорости, ускорения в зависимости от угла поворота кривошипа.
Определяем масштаб угла поворота кривошипа:
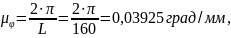
где L - длина угла поворота кривошипа на графике за один оборот, мм.
После построения определим масштабный коэффициент каждой диаграммы.
Определяем масштаб диаграммы скоростей:
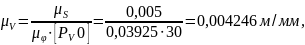
где
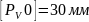 –
полюсное расстояние на графике скорости.
–
полюсное расстояние на графике скорости.
Определяем масштаб диаграммы ускорений:
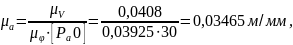
где
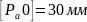 –
полюсное расстояние на графике ускорений,
–
полюсное расстояние на графике ускорений,
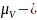 масштабный
коэффициент плана скоростей.
масштабный
коэффициент плана скоростей.
6. Кинетостатический анализ механизма
Определим массу звеньев:
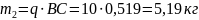 ,
,
где
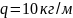 .
.
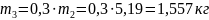
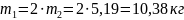
Определяем силы тяжести звеньев:
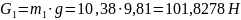
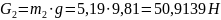
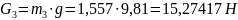
Определяем силы инерции:
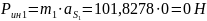
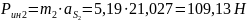
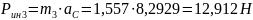 ,
,
где
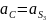
Определяем осевые моменты инерции:

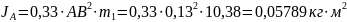
Определяем моменты инерции:
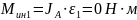
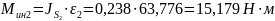

 6.1
Расчет группы Ассура
6.1
Расчет группы Ассура
Отсоединяем группу Ассура от механизма
и прикладываем к ней известные силы, в
том числе и силы инерции, а действия
звеньев и опор заменяем реакциями
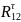 ,
,
 ,
,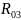 .
.
Определяем давление газов исходя из графика на чертеже:
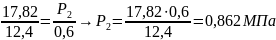
Определим силу, действующую на поршень:
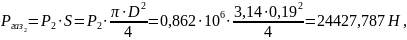
где S – площадь поршня, D – диаметр поршня.
Определим реакции, действующие на шатун:
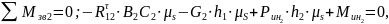
где h1 – плечо силы G2 (16,76 мм), h2 – плечо силы Pин 2 (62,3 мм).
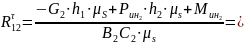

Запишем векторное уравнение для группы Ассура:
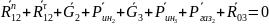
Определим масштабный коэффициент плана сил:
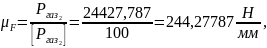
где
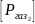 - длина вектора силы
- длина вектора силы
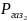 на чертеже.
на чертеже.
Определим длины векторов сил на чертеже:
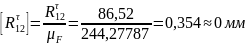
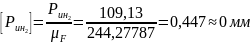
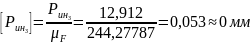
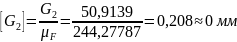
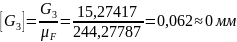
Измерим длины векторов сил и на плане сил:
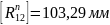
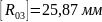
 Определим
истинные значения сил
и
:
Определим
истинные значения сил
и
:
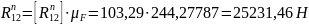
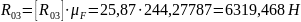
6.2 Расчет ведущего звена
Составим уравнение моментов относительно точки А:
 ,
,
где
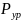 - уравновешивающая сила,
- уравновешивающая сила,
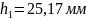 - плечо силы
- плечо силы
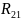
Решим уравнение, приведенное выше:
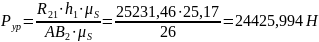
Теперь определим уравновешивающую силу с помощью рычага Жуковского. Для этого построим рычаг Жуковского и запишем уравнение моментов относительно точки A.
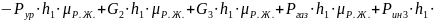
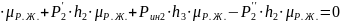 ,
,
где
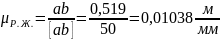 –
масштабный коэффициент рычага Жуковского;
h1
= 50 мм – плечо сил
–
масштабный коэффициент рычага Жуковского;
h1
= 50 мм – плечо сил
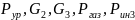 ;
h2
= 12,52 мм – плечо сил
;
h2
= 12,52 мм – плечо сил
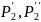 ;
h3
= 7,03 мм – плечо силы
;
h3
= 7,03 мм – плечо силы
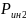 .
.

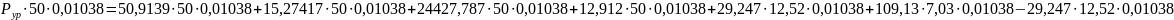
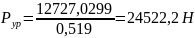
Определяем расхождение результатов уравновешивающей силы:
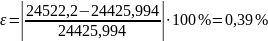
 расхождение
результатов в пределах нормы.
расхождение
результатов в пределах нормы.
7. Синтез кулачкового механизма
Исходные данные:
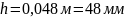
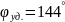
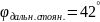
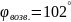
Определим угол ближнего стояния:
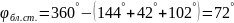
Д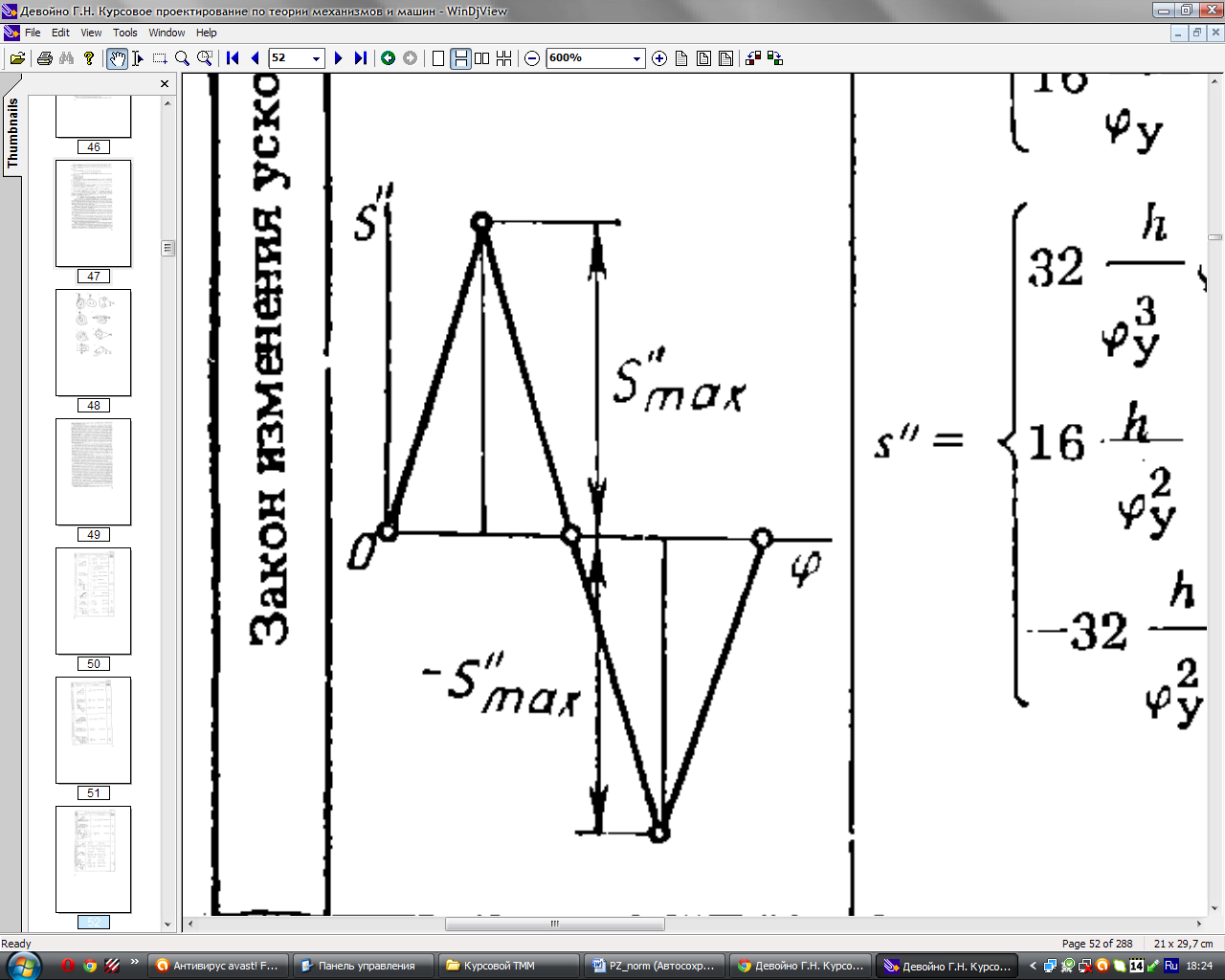
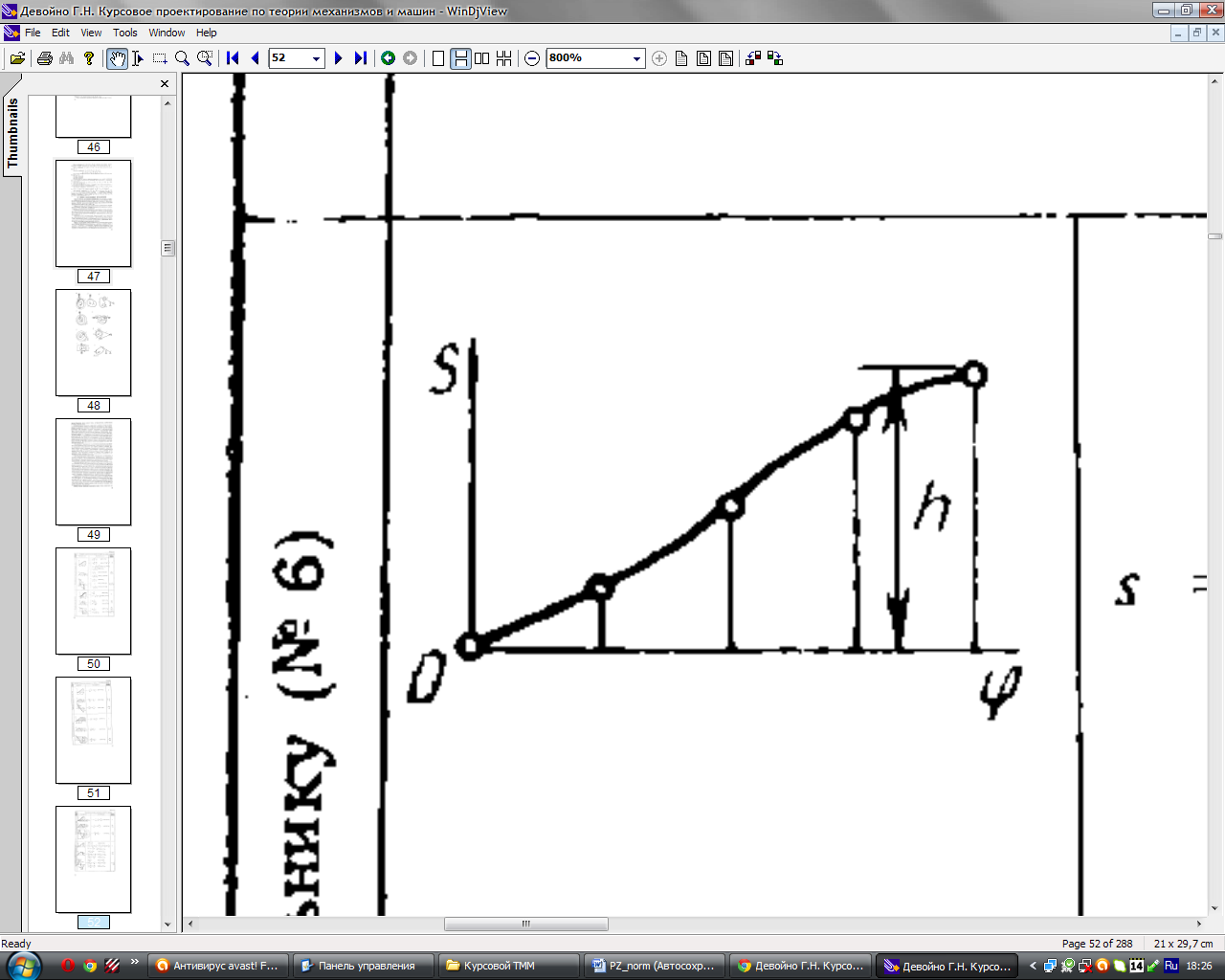 ля
задания движения выходного звена
используем закон изменения ускорения
по треугольнику (рис. 2).
ля
задания движения выходного звена
используем закон изменения ускорения
по треугольнику (рис. 2).
Рис. 2 – Графики закона изменения ускорения по треугольнику
Расчет перемещения S на фазе
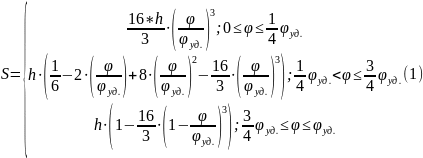
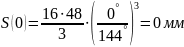
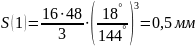
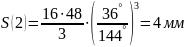
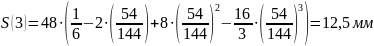
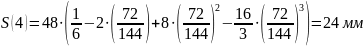

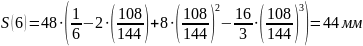
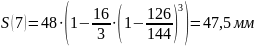
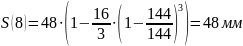
 Результаты
расчета перемещения на фазе
Результаты
расчета перемещения на фазе
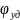 приведены в таблице 8.
приведены в таблице 8.
Перемещения
S
на фазе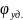 Таблица 8.
Таблица 8.
Координаты № положения |
x |
y, мм |
0 |
|
0 |
1 |
|
0,5 |
2 |
|
4 |
3 |
|
12,5 |
4 |
|
24 |
5 |
|
35,5 |
6 |
|
44 |
7 |
|
47,7 |
8 |
|
48 |
 Расчет
перемещения S
на фазе
Расчет
перемещения S
на фазе
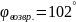
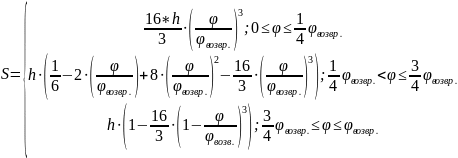
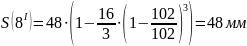
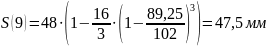
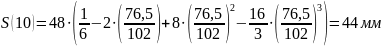
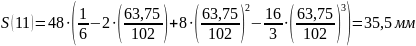
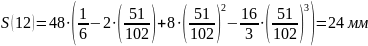
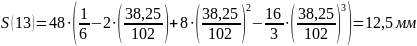
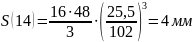

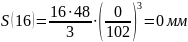
Результаты
расчета перемещения на фазе
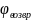 приведены в таблице 9.
приведены в таблице 9.
П еремещения
S
на фазе
еремещения
S
на фазе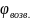 Таблица 9.
Таблица 9.
Координаты № положения |
x |
Расчет - х |
y, мм |
|
|
|
48 |
9 |
|
|
47,5 |
10 |
|
|
44 |
11 |
|
|
35,5 |
12 |
|
|
24 |
13 |
|
|
12,5 |
14 |
|
|
4 |
15 |
|
|
0,5 |
16 |
|
|
0 |
Расчет
ускорений
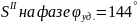
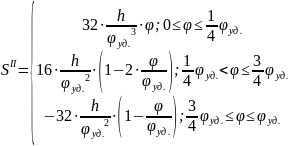
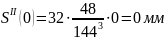
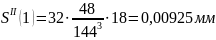
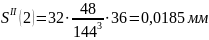
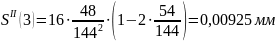
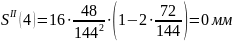
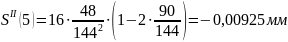
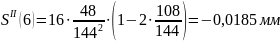
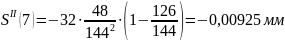

 Результаты
расчета ускорений на фазе
приведены в таблице 10.
Результаты
расчета ускорений на фазе
приведены в таблице 10.
Ускорения на фазе . Таблица 10.
Координаты № положения |
x |
y, мм |
0 |
|
0 |
1 |
|
0,00925 |
2 |
|
0,0185 |
3 |
|
0,00925 |
4 |
|
0 |
5 |
|
-0,00925 |
6 |
|
-0,0185 |
7 |
|
-0,00925 |
8 |
|
0 |
Расчет
ускорений
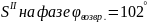
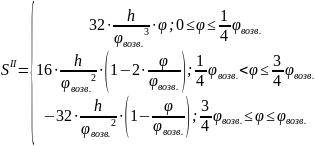
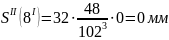
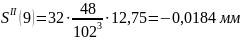


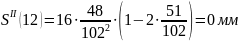

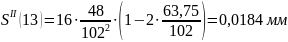
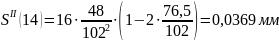
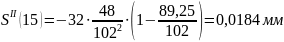

Результаты расчета ускорений на фазе приведены в таблице 11.
Ускорения на фазе Таблица 11.
Координаты № положения |
х |
Расчет - х |
y, мм |
|
|
|
0 |
9 |
|
|
-0,0184 |
10 |
|
|
-0,0369 |
11 |
|
|
-0,0184 |
12 |
|
|
0 |
13 |
|
|
0,0184 |
14 |
|
|
0,0369 |
15 |
|
|
0,0184 |
16 |
|
|
0 |
Расчет кулачкового механизма производился с помощью программы APM. Результат проектирования кулачка см. приложение №1 и чертеж 1.002.00.00 КР ТММ.