МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт математики и компьютерных наук

Кафедра математического моделирования

Реферат на тему «Временные ряды и их применение»

Выполнил: Рыбьяков А.С.,

студент 362 гр.

Проверил: Няшин А.Ф.,

к.ф.-м.н., доцент

Тюмень-2010

Содержание

Введение 3

Глава 1. Теоретические сведение о временных рядах. 5

П.1 Временные ряды. 5

П.2 Процесс белого шума 10

П.3 Процесс авторегрессии 13

П. 4 Процесс скользящего среднего 16

П.5 Нестационарные временные ряды 18

П.7 Тренд и его анализ. 23

П. 8 Автокорреляция уровней временного ряда 24

Глава 2. Пример анализа временного ряда 26

Литература 33

Введение

Временным рядом называют последовательность наблюдений, обычно упорядоченную во времени, хотя возможно упорядочение и по какому-то другому параметру. Основной чертой, выделяющей анализ временных рядов среди других видов статистического анализа, является существенность порядка, в котором призводятся наблюдения. Если во многих задачах наблюдения статистически независимы, то во временных рядах они, как правило, зависимы и характер этой зависимости может определяться положением наблюдений в последовательности. Природа ряда и структура порождающего ряд процесса могут предопределять порядок образования последовательности.

Временной ряд состоит из нескольких компонент: тренд, сезонная компонента, циклическая компонента (стационарный случайный процесс) и случайная компонента.

Под трендом понимается устойчивое систематическое изменение процесса в течение продолжительного времени. Оценка тренда осуществляется параметрическим и непараметрическим методами. Параметрический метод заключается в подборе гладкой функции, которая описывала бы тенденцию ряда: линейный тренд, полином и т.д. Непараметрический метод используется, когда нельзя подобрать гладкую функцию и заключается в механическом сглаживании временных рядов методом скользящей средней. Элементарные методы оценки характеристик временных рядов обычно достаточно подробно рассматриваются в курсах «Общей теории статистики» [1, 2]. Другими словами, тренд – это очищенная от случайностей основная тенденция временного ряда.

Временной ряд обычно колеблется вокруг тренда, причем отклонения от тренда часто обнаруживают правильность. Часто это связано с естественной или назначенной периодичностью, например, сезонной или недельной, месячной или квартальной (например, в соответствии с графиками выплаты зарплаты и уплаты налогов). Иногда наличие периодичности и тем более ее причины неясны, и задача состоит в том, чтобы выяснить, действительно ли имеется периодичность.

Во временных рядах экономических процессов могут иметь место более или менее регулярные колебания. Если они строго периодический или близкий к нему характер и завершаются в течение одного года, то их называют сезонными колебаниями. Оценка сезонной компоненты осуществляется двумя способами: с помощью тригонометрических функций и методом сезонных индексов.

Глава 1. Теоретические сведение о временных рядах. П.1 Временные ряды.

Обычно эконометрические модели строятся на основе двух типов исходных данных:

 данные, характеризующие совокупность различных объектов в

определенный момент (период) времени;

 данные, характеризующие один объект за ряд последовательных

моментов (периодов) времени.

Модели, построенные по данным первого типа, называются

пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.

Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

 факторы, формирующие тенденцию ряда (например, инфляция влияет на увеличение размера средней заработной платы);

 факторы, формирующие циклические колебания ряда (например, уровень безработицы в курортных городах в зимний период выше по сравнению с летним);

 случайные факторы.

Очевидно, что реальные данные чаще всего содержат все три компоненты. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Если же временной ряд представлен как их произведение, то такая модель называется мультипликативной.

Под временным рядом (time series) понимается последовательность наблюдений значений некоторой переменной, произведенных через равные промежутки времени. Если принять длину такого промежутка за единицу времени (год, квартал, день и т.п.), то можно считать, что последовательные наблюдения произведены в моменты .

Основная отличительная особенность статистического анализа временных рядов состоит в том, что последовательность наблюдений рассматривается как реализация последовательности, вообще говоря, статистически зависимых случайных величин , имеющих некоторое совместное распределение с функцией распределения

. (1)

Рассмотриваются в основном временные ряды, у которых совместное распределение случайных величин имеет совместную плотность распределения .

Чтобы сделать задачу статистического анализа временных рядов доступной для практического решения, приходится так или иначе ограничивать класс рассматриваемых моделей временных рядов, вводя те или иные предположения относительно структуры ряда и структуры его вероятностных характеристик. Одно из таких ограничений предполагает стационарность временного ряда.

Ряд , , (в дальнейшем обозначения и будем считать равнозначными) называется строго стационарным (или стационарным в узком смысле), если для любого , совместное распределение вероятностей случайных величин такое же, как и для , при любых и , таких, что и .

Другими словами, свойства строго стационарного временного ряда не изменяются при изменении начала отсчета времени. В частности, при из предположения о строгой стационарности временного ряда следует, что закон распределения вероятностей случайной величины не зависит от , а значит, не зависят от и все его основные числовые характеристики (если, конечно, они существуют), в том числе: математическое ожидание и дисперсия .

Значение . определяет постоянный уровень, относительно которого колеблется анализируемый временной ряд , а постоянная характеризует размах этих колебаний.

Одно из главных отличий последовательности наблюдений,образующих временной ряд, заключается в том, что члены временного ряда являются, вообще говоря, статистически взаимозависимыми. Степень тесноты статистической связи между случайными величинами и может быть измерена парным коэффициентом корреляции

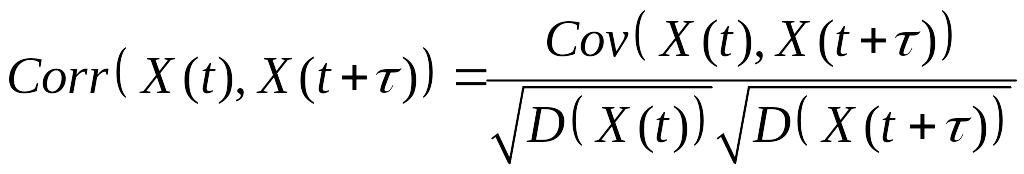, (2)

где

Если ряд стационарный, то значение не зависит от и является функцией только от ; мы будем использовать для него обозначение :

(3)

В частности,

Соответственно, для стационарного ряда и значение коэффициента корреляции зависит только от  ; мы будем использовать для него обозначение так что:

₍₄₎

В частности,

Практическая проверка строгой стационарности ряда xt на основании наблюдения значений в общем случае затруднительна. В связи с этим под стационарным рядом на практике часто подразумевают временной ряд , у которого

(5)

Ряд, для которого выполнены указанные три условия, называют стационарным в широком смысле (слабо стационарным, стационарным второго порядка или ковариационно стационарным).

Если ряд является стационарным в широком смысле, то он не обязательно является строго стационарным. В то же время, и строго стационарный ряд может не быть стационарным в широком смысле просто потому, что у него могут не существовать математическое ожидание и/или дисперсия. (В отношении последнего примером может служить случайная выборка из распределения Коши.) Кроме того, возможны ситуации, когда указанные три условия выполняются, но, например, зависит от . Ряд , , называется гауссовским, если совместное распределение случайных величин является -мерным нормальным распределением. Для гауссовского ряда понятия стационарности в узком и в широком смысле совпадают.

В дальнейшем, говоря о стационарности некоторого ряда , мы (если не оговаривается противное) будем иметь в виду, что этот ряд стационарен в широком смысле (так что у него существуют математическое ожидание и дисперсия). Итак, пусть – стационарный ряд c

₍₆₎

Поскольку в данном случае коэффициент измеряет корреляцию между членами одного и того же временного ряда, его принято называть коэффициентом автокорреляции (или просто автокорреляцией). По той же причине о ковариациях говорят как об автоковариациях. При анализе изменения величины в зависимости от значения принято говорить об автокорреляционной функции .

Автокорреляционная функция безразмерна, т.е. не зависит от масштаба измерения анализируемого временного ряда. Ее значения могут изменяться в пределах от до ; при этом . Кроме того, из стационарности ряда следует, , так что при анализе поведения автокорреляционных функций обычно ограничиваются рассмотрением только неотрицательных значений .

График зависимости часто называют коррелограммой. Он может использоваться для характеризации некоторых свойств механизма, порождающего временной ряд. При этом заметим, что если – стационарный временной ряд и – некоторая постоянная, то временные ряды и имеют одинаковые коррелограммы.

Если предположить, что временной ряд описывается моделью стационарного гауссовского процесса, то полное описание совместного распределения случайных величин требует задания параметров: или

Это намного меньше, чем без требования стационарности, но все же больше, чем количество наблюдений. В связи с этим, даже для стационарныхгауссовских временных рядов приходится производить дальнейшее упрощение модели с тем, чтобы ограничить количество параметров, подлежащих оцениванию по имеющимся наблюдениям. Мы переходим теперь к рассмотрению некоторых простых по структуре временных рядов, которые, в то же время, полезны для описания эволюции во времени многих реальных экономических показателей.