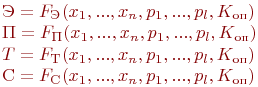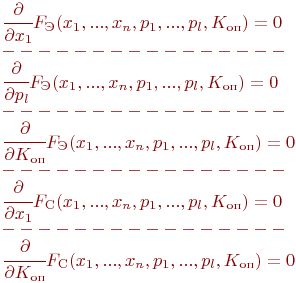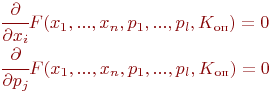6.3. Решение задачи оптимизации

Во многих практических ситуациях связь между технологическими факторами и параметрами носит довольно сложный характер, что делает задачу получения ее адекватного математического описания чрезвычайно трудной. Эти затруднения еще дополнительно усиливаются из-за многомерности исследуемого процесса (большого количества факторов, влияющих на параметр оптимизации ) и высокого уровня "производственного шума".

При невозможности получения адекватного математического описания исследуемого процесса наиболее приемлемым методом поиска оптимальных условий его проведения является метод эмпирической оптимизации, основанный на том, что изменение значений технологических факторов процесса производится лишь после анализа предшествующих ситуаций. Иными словами, решение о переносе условий эксперимента в другую точку факторного пространства принимается по результатам предыдущих экспериментов. При этом однозначно определяются и координаты новой точки.

Идея этого метода, получившего название симплексного метода планирования и его модификаций, положена в основу многих практических задач оптимизации. Наиболее приемлемым методом при проектировании является метод Нелдера - Мида. Разновидности симплексных методов описаны в специальной литературе.

За оптимизируемую функцию принимается критерий качества . Например, для технологического процесса изготовления ВКУ, изображенного на рис. 4.1, схема оптимизации имеет вид, показанный на рис. 6.2.

На вход схемы подаются исходные данные . В блоке "Расчет признаков готовой продукции" производится расчет уравнений регрессии. Получаются значения по математической модели (для всех показателей качества ). На данном этапе можно говорить о прогнозировании качества, но не управлении им.

В блоке "Формирование обобщенного показателя качества " идет формирование обобщенного показателя в аддитивной форме.

Рис. 6.2.  Схема проведения оптимизации параметров ТП изготовления ВКУ

В блоке " ?" происходит сравнение обобщенного показателя качества с оптимальным значением. Если , то переходим к формированию экономических показателей. Обычно это отношение должно быть близко к 1, но, как и в случае к.п.д., единицы не достигает. Поэтому в алгоритме заложено правило останова: процесс поиска оптимальных параметров прекращается, если он не приводит к улучшению обобщенного критерия качества. Если условие не выполняется, то производится поиск оптимального соотношения параметров: варьируют значения параметров в рамках технологических допусков.

Условием состоятельности обобщенного показателя является соответствие его целям управления качеством продукции. Поэтому расчет такого показателя должен проводиться в соответствии с картой технического уровня с учетом перспективных показателей качества.

6.4. Формирование экономических критериев управления производством

Если учесть, что любой производственный процесс должен отвечать требованиям увеличения производительности при минимальных затратах и минимальной себестоимости продукции, то такой процесс характеризуется следующими целевыми функциями или критериями управления:

- энергоемкость производства;

- производительность труда;

- трудозатраты;

- себестоимость.

Для получения оптимальных значений критериев управления необходим выбор оптимальной совокупности параметров процесса. Так как каждый из указанных критериев в общем виде является сложной функцией входных и выходных параметров процесса, то

(6.18)

где - входные параметры процесса;

- выходные параметры процесса (готовой продукции);

- обобщенный критерий качества.

Необходимым условием выбора параметров , , , обеспечивающим экстремальные значения критериев ( , , , ), является равенство нулю первых частных производных функций по параметрам

(6.19)

Для решения системы уравнений (6. 19) и проверки их соответствия оптимальности используется метод неопределенных множителей Лагранжа.

В целях упрощения решения правомерно проведение исследований по небольшим группам параметров. Как показано в теории математического программирования, такие величины (кроме специальных случаев вырождения и др.) равны соответствующим оптимальным значениям двойственных переменных, т. е.

(6.20)

Составление и решение уравнений (6.20) в частных производных дает возможность составления парных уравнений с одноименными параметрами

(6.21)

Совместное решение этих уравнений позволяет найти численные значения параметров , удовлетворяющие оптимальным условиям (рис. 6.3). В пределах области находятся все значения частных решений.

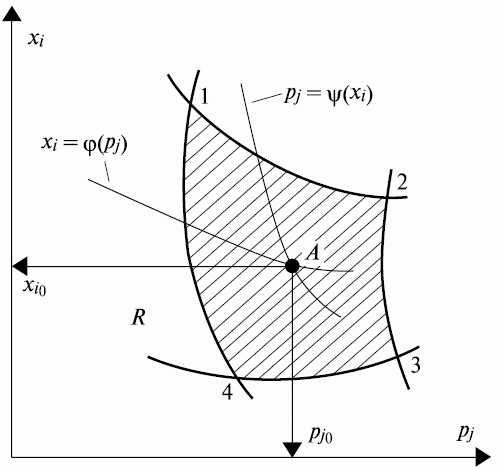
Рис. 6.3.  Связь показателей качества с параметрами технологического процесса

Частным видом парных уравнений являются уравнения регрессии, совместное решение которых может дать искомый результат.

После решения задачи оптимизации экономических показателей общая схема оптимизации производства, представленная на рис. 6.2, примет вид, представленный на рис. 6.4.

увеличить изображение Рис. 6.4.  Схема производства ВКУ с учетом Коп и Купр производством