ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОМНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

КОНСПЕКТ

«Психологический анализ в среде Excel» Сапегин А.Г.

Выполнили:

Студенты 1 курса 1 группы

Факультета психологии

Пронина Анна Вячеславовна

Цыбенко Олег Андреевич

Ростов-на-Дону

2013 г.

КОНСПЕКТ

«Психологический анализ в среде Excel» Сапегин А.Г.

(Программа 1)

1. Основы измерения и количественного описания данных - рассматриваемый нами источник данный вопрос не включает

2. Общие принципы проверки статистических гипотез. Введение в проблему статистического вывода

Статистические гипотезы.

При обработке материалов исследования психолог выдвигает гипотезы, которые систематизируют его предположения и представляют их в четком и лаконичном виде.

Проверка статистической гипотезы - рассматриваемый нами источник данный вопрос не включает

Нулевая и альтернативная гипотезы.

Статистические гипотезы делятся на нулевые (Н₀) и альтернативные (Н₁ ).

Гипотеза Н₀ – это гипотеза об отсутствии различий, например: уровень физической агрессии у юношей и девушек одинаковый.

Гипотеза Н₁ – это гипотеза о значимости различий, например: уровень физической агрессии у юношей выше, чем у девушек.

Понятие уровня статистической значимости.

Уровень значимости - это вероятность (α) отклонения нулевой гипотезы, в то время как она верна. Другими словами – это уверенность в принятии гипотезы Н_1. То есть, чем выше уровень значимости, тем выше уверенность в правильности принятия гипотезы Н₁, и тем меньше вероятность совершить при этом ошибку.

Ось значимости.

В практике статистических измерений в психологии принято считать низшим уровнем статистической значимости 5% - ный уровень (α≤0,05); достаточным 1% - ный уровень (α≤0,01) и высшим уровнем 0,1% (α≤0,001).

Статистический критерий и число степеней свободы.

Статистический критерий – это решающее правило принятия истинной и отклонения ложной гипотезы с высокой вероятностью.

Критерии делятся на параметрические и непараметрические. Параметрические критерии включают в формулу расчета параметры распределения изучаемого признака такие, как среднее, стандартное отклонение и дисперсию. К параметрическим критериям относятся критерии t-Стьюдента и линейный коэффициент корреляции по Пирсону.

Проверка гипотез с помощью статистических критериев

Способность критерия отклонять нулевую гипотезу об отсутствии различий, если она не верна, называется мощностью критерия. Мощность критерия определяется эмпирическим путем. Одна и та же задача может быть решена с помощью различных критериев, при этом обнаруживается, что одни критерии позволяют выявить различия, а другие нет. Из двух критериев, используемых для решения задачи, доверия заслуживает тот, который смог отклонить нулевую гипотезу. Если же первый и второй критерии подтвердили нулевую гипотезу, то доверия заслуживают оба.

Статистическое решение и вероятность ошибки - рассматриваемый нами источник данный вопрос не включает Направленные и ненаправленные гипотезы - рассматриваемый нами источник данный вопрос не включает

Этапы принятия статистического решения - рассматриваемый нами источник данный вопрос не включает

Классификация психологических задач, решаемых с помощью статистических методов - рассматриваемый нами источник данный вопрос не включает

Корреляционный анализ.

Понятие корреляционной связи.

Связь именуется корреляционной или вероятностной в том случае, когда каждому значению одного признака соответствует несколько более или менее отличных значений другого признака.

Виды корреляционных связей.

Степень варьирования значений одного признака при данном значении другого может быть различной, если эта степень варьирования относительно мала, то связь близка к функциональной. При большом варьировании связь между изучаемыми явлениями менее выражена, степень связи меньше. Если любому значению одного признака может соответствовать любое значение другого признака, то связь между такими признаками отсутствует. Корреляционные связи бывают разной степени выраженности, разной степени тесноты. Max теснота связи - функциональная связь, min – отсутствие связи. Степень тесноты связи может быть выражена с помощью специальных коэффициентов корреляции.

Положительная, отрицательная и другие виды корреляций

При положительной корреляции при увеличении числовых значений одного признака соответственно увеличиваются числовые значения другого признака. При отрицательной корреляции увеличению числовых значений одного признака соответствует уменьшение числовых значений другого признака.

Выбросы - рассматриваемый нами источник данный вопрос не включает

Задача корреляционного анализа: установление направления (положительное, отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками. - рассматриваемый нами источник данный вопрос не включает

Коэффициент линейной корреляции 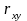Пирсона.

Коэффициент линейной корреляции показывает, существует ли и сколь велика связь между двумя взаимозависимыми признаками. К.к. принимает значения от -1 до +1. Если никакой связи между признаками не существует, то коэффициент равен 0.

Пример: Приводятся данные о продолжительности ознакомления (в секундах) и времени восприятия (в секундах) системы пространственных линий.

Ознакомление Х: 2,5 1,9 3,7 2,0 4,3 2,4 2,3 4,8 1,7 3,2 3,6 2,3 4,9 1,8 2,8 4,0 1,8 3,0 2,4 4,5 2,3 3,4 2,0 2,5; n₁ = 24 Восприятие Y: 3,2 1,5 2,4 3,6 4,5 3,0 3,1 4,2 2,9 3,5 4,0 3,0 4,3 2,5 2,9 3,6 2,5 3,2 2,9 3,9 2,7 3,6 2,4 3,0; n₂ = 24 Что можно сказать о существовании связи между этими параметрами деятельности?

Для решения этой задачи с помощью линейного коэффициента корреляции по Пирсону составим таблицу.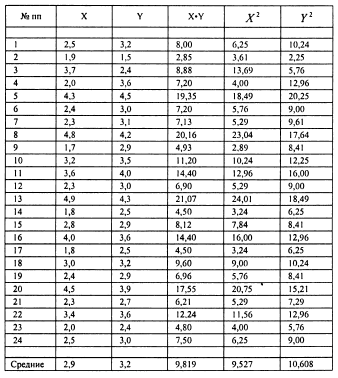

Вычисление средних выполняется по следующим формулам: где средние значения. Стандартное отклонение _x и _y будем вычислять по формулам: и . Подставив в последние формулы числовые значения, получим _x =0,983, а _y = 0,689. Вычислим линейный коэффициент корреляции по Пирсону по формуле: . Проверим надежность вычисленного значения коэффициента r по формуле: . Для числа степеней свободы v=∞ по таблице критерия t-Стьюдента найдем t_кр. . Сравним t_э с t_кр..Видим ,что t_э >t_кр, а это означает, что связь между параметрами ознакомление и восприятие существует значимо на уровне значимости 1% . Решим эту задачу в Excel.

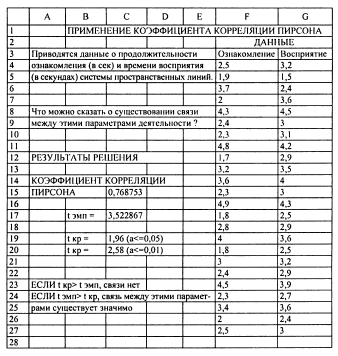
При этом в соответствующие ячейки записываются следующие формулы:

(C15)--->=ПИРСОН(F4:F27;G4:G27) (C17)--->=ABS(C15)*КОРЕНЬ(24-3), где 24 – объем данных. Из сравнения t_эмп с t_кр видно, что t_эмп > t_кр на уровне значимости α≤0,01, т.е. принимается гипотеза Н₁ на уровне значимости 1%. Н₁ означает, что корреляция между изучаемыми параметрами деятельности отличается от 0, т.е. присутствует на уровне значимости 1%.

Ранговый коэффициент корреляции 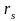Спирмена.

Используется для определения тесноты связи между признаками в случае их количественного представления. Для определения рангового коэффициента корреляции необходимо проранжировать (в убывающем или возрастающем порядке) все значения признака Х и вместе с тем записывают соответствующие значения признака Y. Затем определяют ранг по обоим признакам, т.е. номер каждого ранжированного признака в ранжированных рядах. Для равных значений признака ранг находится путем деления суммы приходящихся на них рангов на число равных значений. К.к рангов вычисляется по формуле: где n – число коррелируемых пар значений признаков X,Y; d_i – разность рангов I – того испытуемого в первом и втором ранговом ряду. Коэффициент корреляции рангов принимает значения от -1 до +1. Если никакой связи между признаками не существует, то коэффициент равен 0.

Покажем решение предыдущей задачи с помощью коэффициента корреляции рангов по Спирмену. Составим следующую таблицу:

По таблице коэффициента корреляции рангов по Спирмену найдем критическе значения для n=24.

Сравним pэ с ркр. Видим, что рэ>p кр, а это означает, что принимается гипотеза Н1, т.е связь между параметрами ознакомление и восприятие существует значимо на уровне значимости 1% (α≤0,01).

Решим эту задачу ранговым коэффициентом корреляции в среде Excel:

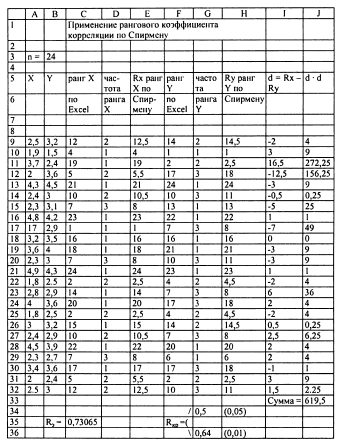
При этом в соответствующие ячейки записываются следующие формулы:

Из сравнения Rэ с Rкр видно, что Rэ>Rкр на уровне значимости α≤0,01, т.е. принимается гипотеза Н1 на уровне значимости 1%. Н1 означает, что корреляция между изучаемыми параметрами деятельности отличается от 0, т.е. присутствует на уровне значимости 1 %

Случай одинаковых рангов - рассматриваемый нами источник данный вопрос не включает