
- •Глава 1
- •Глава 2
- •§1 Оптимизация плана производства Цели
- •§ 2 Оптимальное смешение
- •§ 3 Оптимальный раскрой Цели
- •1 . Определение рациональных способов раскроя материала.
- •2. Определение интенсивности использования рациональных спо собов раскроя.
- •§ 4 Планирование финансов Цели
- •2. Открытая транспортная задача.
- •§ 6 Задача о назначениях Цели
§ 2 Оптимальное смешение
Цели
В данном параграфе показаны возможности использования модели линейного программирования для решения задач оптимального смешения. Наряду с рассмотренной в главе 1 задачей планирования производства это одна из наиболее известных областей приложения модели линейного программирования. Модели оптимального смешения имеют много общего с моделями оптимального планирования производства. В то же время существуют и некоторые особенности.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь формулировать и использовать для экономического анализа следующие понятия:
смесь;
ингредиент смеси;
компонент смеси;
рецепт смешения.
Модели
Важный класс прикладных оптимизационных задач образуют задачи о смесях. Такие задачи возникают при выборе наилучшего способа смешения исходных ингредиентов для получения смеси с заданными свойствами. Смесь должна иметь требуемые свойства, которые определяются количеством компонентов, входящих в состав исходных ингредиентов. Как правило, известны стоимостные характеристики ингредиентов и искомую смесь требуется получить с наименьшими затратами. Для многопродуктовых задач, в которых требуется получить несколько смесей, характерным является критерий максимизации прибыли.
Задачи оптимального смешения встречаются во многих отраслях промышленности (металлургия, парфюмерия, пищевая промышленность, фармакология, сельское хозяйство). Примерами задач о смесях могут служить определение кормового рациона скота на животноводческих фермах, составление рецептуры шихты на металлургическом производстве и т.п. Рассмотрим сначала однопродуктовые модели оптимального смешения.
Введем обозначения:
п — количество исходных ингредиентов;
т — количество компонентов в смеси
xj — количество j-го ингредиента, входящего в смесь;
аij — количество i-го компонента в j-м ингредиенте;
cj — стоимость единицы j-го ингредиента;
bi — количество i-го компонента в смеси.
Модель A:
→ min, (1)
i =1,...,m, (2)
xj>0, j= 1,..., п. (3)
Здесь (1) — целевая функция (минимум затрат на получение смеси);
(2) — группа ограничений, определяющих содержание ком-
понентов в смеси;
(3) — ограничения на неотрицательность переменных.
В задаче могут присутствовать также ограничения на общий объем смеси и ограничения на количество используемых ингредиентов. Эти группы ограничений, а также ограничения (2) характерны для задачи планирования производства, рассмотренной в параграфе 1.
Введем обозначения:
п — количество исходных ингредиентов;
т — количество компонентов в смеси;
w — количество условий, отражающих содержание j-го ингредиента в смеси;
xj — количество j-ro ингредиента, входящего в смесь;
аij — доля i-го компонента в j-м ингредиенте;
bi — минимально допустимая доля i-го компонента в смеси;
сj — стоимость единицы j-го ингредиента;
drj — коэффициент, отражающий r-е условие на содержание j-го ингредиента в смеси.
Модель В:
→ min, (4)
 ,
j=1,..., m, (5)
,
j=1,..., m, (5)
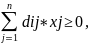 r=1,...,w
,
(6),
r=1,...,w
,
(6),
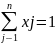 (7)
(7)
 (8)
(8)
Здесь (4) — целевая функция (минимум затрат на получение смеси);
(5) — группа ограничений, определяющих содержание
компонентов в смеси;
(6) — группа ограничений на содержание ингредиентов в
смеси;
— ограничение на количество смеси;
— ограничения на неотрицательность переменных.
Ограничения (5) и (6) отличают задачу смешения от задачи оптимального планирования производства. Заметим, что значения правых частей этих ограничений равны нулю. Вектор х* с компонентами х*, являющийся решением этой оптимизационной задачи, называют рецептом приготовления смеси или рецептом смешения.
