
- •Содержание
- •Предисловие
- •1.1. Термины и понятия
- •1.2. Принципиальная схема автоматического управления
- •1.3. Принципы управления
- •1.4. Задачи теории автоматического управления
- •Литература
- •2.1. Дифференциальное и операторное уравнения, передаточная функция и характеристическое уравнение разомкнутой системы
- •2.2. Частотные характеристики
- •2.3. Математические модели входных воздействий
- •2.4. Переходная функция
- •Литература
- •3.1 Усилительное звено
- •3.2. Запаздывающее звено
- •3.3. Инерционное звено
- •Построение выполняется по формуле
- •Вначале находим координаты пересечения:
- •Построение выполняется по формуле
- •3.4. Интегрирующее звено
- •3.5. Дифференцирующее звено
- •Комплексная частотная характеристика
- •Логарифмическая амплитудная частотная характеристика
- •3.6. Колебательное звено
- •В случае ξ 0,3 нужно пользоваться точной лачх из-за возрастания амплитуды в окрестности резонансной частоты.
- •3.7. Апериодическое звено второго порядка
- •3.8. Классификация типовых звеньев
- •Литература
- •4.1. Построение и анализ структурных схем
- •4.2. Передаточные функции систем
- •4.2.1. Последовательное соединение звеньев
- •4.2.2. Параллельное соединение звеньев
- •4.2.3. Система с обратной связью
- •4.2.4. Передаточная функция разомкнутой системы
- •4.2.5. Передаточная функция замкнутой системы
- •4.2.6. Передаточная функция по ошибке
- •4.2.7. Передаточная функция по возмущению
- •4.2.8. Передаточные функции системы с перекрестными связями
- •4.3. Статические и астатические системы
- •4.4. Перестановка структурных элементов
- •4.4.1. Перестановка узлов и сумматоров
- •4.4.1.1. Перенос узла через узел
- •4.4.1.2. Перенос сумматора через сумматор
- •4.4.1.3. Перенос сумматора через узел по направлению передачи сигнала
- •4.4.1.4. Перенос сумматора через узел против направления передачи сигнала
- •4.4.2. Перенос узла или сумматора через звено
- •4.4.2.1. Перенос узла с выхода звена на вход
- •4.4.2.2. Перенос узла с входа звена на выход
- •4.4.2.3. Перенос сумматора с выхода звена на вход
- •4.4.2.4. Перенос сумматора с входа звена на выход
- •5.1. Понятие об устойчивости
- •Записываем операторное уравнение
- •5.2. Критерий Гурвица Для характеристического уравнения
- •5.3. Критерий Михайлова
- •Находим передаточную функцию замкнутой системы
- •5.4. Критерий Найквиста
- •Литература
- •6.1. Прямые показатели качества
- •6.2. Косвенные показатели качества
- •6.4. Апериодический процесс с колебательной составляющей
- •Интегральные оценки качества Первая интегральная оценка:
- •6.3. Чувствительность к изменению параметров
- •Литература
- •7.1. Понятие синтеза системы
- •7.2. Коррекция систем
- •7.2.1. Последовательная коррекция
- •7.2.2. Параллельная коррекция
- •7.2.3. Коррекция по возмущению
- •7.2.4. Коррекция времени регулирования
- •Корректирующими звеньями
- •7.3. Синтез типовых регуляторов
- •Литература
- •Приложение
- •Разомкнутая система управления – система, выходная величина которой не влияет на ее вход.
- •Гильфанов Камиль Хабибович Подымов Владимир Николаевич
3.5. Дифференцирующее звено
Сначала рассмотрим идеальное дифференцирующее звено. Дифференциальное уравнение этого звена устанавливает пропорциональность выходной величины скорости изменения входной величины:
![]() .
(3.5)
.
(3.5)
Операторное уравнение: Y(p) = kp X(p).
Передаточная функция
![]()
где k – коэффициент, имеющий размерность времени.
Комплексная частотная характеристика
![]() .
.
Действительная часть U(ω) = 0, мнимая часть V(ω) = k ω.
Амплитудная частотная характеристика
![]() .
.
Амплитуда растет линейно с частотой.
Фазовый угол для всех частот 90, что означает постоянное опережение по фазе при любой частоте.
Переходная функция – в ответ на единичное ступенчатое воздействие – имеет вид:
![]()
То есть, на выходе появляется единичный импульс, усиленный в k раз.
Осуществить практически идеальное дифференцирующее звено невозможно. Но реализуемы математические модели, в которых присутствует дифференцирующая составляющая dx/dt. Так, если записать в правой части инерционного звена вместо усилительного дифференцирующее воздействие, получается математическая модель, которую называют «реальное дифференцирующее звено».
![]() (3.6)
(3.6)
Операторное уравнение: (Tp + 1)Y(p) = kpX(p).
Передаточная функция
![]() .
.
Комплексная частотная характеристика
![]() .
.
Действительная и мнимая частотные характеристики
![]() ,
, ![]() .
.
Амплитудная частотная характеристика
![]() .
.
У идеального дифференцирующего звена с увеличением ω амплитуда линейно возрастает до ∞. У реального дифференцирующего звена амплитуда возрастает монотонно, стремясь к пределу k/T.
Фазовая частотная характеристика
φ(ω)
= arctg![]() .
.
При ω = 0, φ = 90, как у идеального дифференцирующего звена. Но мере увеличения частоты опережение по фазе уменьшается до нуля.
Логарифмическая амплитудная частотная характеристика
![]() .
.
Найдем
асимптотические прямые логарифмической
амплитудной частотной характеристики.
В области ω
< 1
![]() .
В области ω
> 1 L2
= 20 lg
(k/T).
.
В области ω
> 1 L2
= 20 lg
(k/T).
Прямая L1 пересекает ординату в точке с координатами lg ω = 0, L1 = 20 lg k, абсциссу – в точке с координатами lg ω = lg(1/k), L1 = 0. Cледует учесть, что k 1 и потому lg (1/k) – число отрицательное. Прямая L2 параллельна оси абсцисс, пересекает ординату в точке lg ω = 0, L2 = 20 lg(k/T). Прямые L1 и L2 пересекаются в точке с абсциссой lg ω = lg (1/T). График представлен на рис. 3.6.

Рис. 3.6. Асимптоты ЛАЧХ реального дифференцирующего звена
Чтобы найти переходную функцию, в операторном уравнении заменим X(p) на 1/p:
![]() .
.
Таблица преобразований Лапласа указывает, что
![]() .
.
Значит, переходная функция имеет вид
![]() .
.
В момент t = 0 h(0) = k/T. По мере увеличения t, функция h(t) экспоненциально уменьшается до нуля. Напомним: в идеальном дифференцирующем звене переходная функция имеет вид импульса.
3.6. Колебательное звено
Математической моделью колебательного звена является линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
![]() ,
(3.7)
,
(3.7)
при
условии
![]() .
.
Колебательные процессы характеризуются двумя важными параметрами: коэффициентом затухания ξ и резонансной частотой ω0. Они выражаются через постоянные времени уравнения (3.7): ξ = Т0/2Т, ω0 = 1/Т. Если ввести ξ в уравнение (3.7), оно получает вид, более удобный для исследования колебательного процесса:
![]() 2
ξ
Т
2
ξ
Т
![]() + y
= kx.
(3.8)
+ y
= kx.
(3.8)
Дифференциальному уравнению (3.8) соответствует операторное уравнение
(T2p2 + 2 ξ Tp + 1) Y(p) = kX(p),
из которого получается передаточная функция
![]() .
.
Если выходная величина не изменяется (dy/dt = 0, p = 0) передаточная функция вырождается в коэффициент усиления: K(0) = k.
Комплексная частотная характеристика звена
![]() .
.
Действительная и мнимая частотные характеристики имеют вид:
![]() ,
,
![]() .
.
Амплитудная частотная характеристика колебательного звена
![]() .
.
У колебательного звена кривая A(ω) имеет пик, вершина которого отвечает частоте ω0 = 1/T (рис. 3.7). То есть резонансной частоте. Максимальная величина амплитуды равна k / 2ξ. Пик выше, если больше коэффициент усиления и меньше коэффициент затухания.
Фазовая частотная характеристика в интервале изменения частоты от ω = 0 до ω = 1/T рассчитывается по формуле
![]()
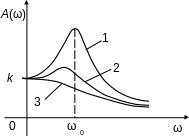
Рис. 3.7. Зависимость амплитуды от частоты.
1 – ξ = 0,20, 2 – ξ = 0,5, 3 – ξ = 0,75

Рис. 3.8. Фазовая частотная характеристика колебательного звена.
1 – ξ = 0,2, 2 – ξ = 0,4, 3 – ξ= 0,8

Рис. 3.9. Асимптотическая ЛАЧХ в интервале 0,3 < ξ < 1
При ω = 0 φ(ω) = 0. Значению ω0 = 1/T соответствует запаздывание – 90 . С увеличением ω запаздывание увеличивается и расчет надо вести по формуле
 .
.
Характер кривых показан на рис. 3.8.
Логарифмическая амплитудная частотная характеристика имеет вид:
L(ω) = 20 lg k – 10 lg (1-T2ω2)2 + 4 ξ2T2ω2.
Форма
этой кривой зависит от коэффициента
затухания ξ.
В интервале 0,3
ξ
1 приемлемо асимптотическое представление.
В области ω
1 L1
= 20 lgk.
В области ω
1 L2 = 20
lg (k/T2)
– 40 lg
ω.
Условие сопряжения прямых ω0 = 1/T,
т.е. на резонансной частоте. Пересечение
прямой L2
c
осью абсцисс при ω
=![]() /T.
Расположение асимптотических прямых
показано на рис. 3.9.
/T.
Расположение асимптотических прямых
показано на рис. 3.9.
