Раздел 3. Основы математического анализа

Тема 3.1 Теория пределов. Непрерывность функции

Предел функции. Свойства предела функции. Односторонние пределы. Предел суммы, произведения и частного двух функций. Непрерывные функции, их свойства. Непрерывность элементарных и сложных функций. Замечательные пределы. Бесконечно большие и бесконечно малые функции. Эквивалентные бесконечно малые функции. Непрерывность функции. Точки разрыва, их классификация.

Тема 3.2. Дифференциальное исчисление функции одной действительной переменной

Определение производной функции. Производные основных элементарных функций. Дифференцируемость функции. Дифференциал функции. Производная сложной функции. Правила дифференцирования: производная суммы, произведения и частного. Производные и дифференциалы высших порядков. Раскрытие неопределенностей, правила Лопиталя. Возрастание и убывание функций, условия возрастания и убывания. Экстремумы функций, необходимое условие существования экстремума. Нахождение экстремумов с помощью первой производной. Выпуклые функции. Точки перегиба. Асимптоты. Полное исследование функции.

Тема 3.3. Интегральное исчисление функции одной действительной переменной

Неопределенный интеграл, его свойства. Таблица основных интегралов. Метод замены переменных. Интегрирование по частям. Интегрирование рациональных функций. Интегрирование некоторых иррациональных функций. Универсальная подстановка.

Определенный интеграл, его свойства. Основная формула интегрального исчисления. Интегрирование заменой переменной и по частям в определенном интеграле. Приложения определенного интеграла в геометрии.

Задания контрольной работы

Задание 1. Матрицы.

Даны матрицы А и В. Найти:

а) линейную комбинацию матриц ;

б) произведение матриц

1. А= , В= .

2. А= , В=

3. А= , В=

4. А= , В=

5. А= , В=

6. А= , В=

7. А= , В=

8. А= , В=

9. А= 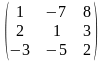, В=

10. А= , В=

Задание 2. Системы линейных уравнений.

Решить систему линейных уравнений:

а) матричным методом;

б) по формулам Крамера;

в) методом Гаусса.

1.

2.

3.

4.

5.

6.

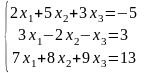
7.

8.

9.

10.

Задание 3. Векторы. Уравнение прямой.

Даны вершины треугольника АВС: А, B, C. Найти:

а) уравнение стороны АВ;

б) уравнение высоты CH;

в) уравнение медианы AM;

г) расстояние от точки С до прямой АВ;

д) угол при вершине А;

е) площадь треугольника АВС.

1. А(-2;4), B(3;1), C(10;7).

2. А(-3;-2), B(14;4), C(6;8).

3. А(1;7), B(-3;-1), C(11;-3).

4. А(1;0), B(-1;4), C(9;5).

5. А(1;-2), B(7;1), C(3;7).

6. А(-2;-3), B(1;6), C(6;1).

7. А(-4;2), B(-6;6), C(6;2).

8. А(4;-3), B(7;3), C(1;10).

9. А(4;-4), B(8;2), C(3;8).

10. А(-3;-3), B(5;-7), C(7;7).

Задание 4. Кривые второго порядка

По уравнению кривой второго порядка определить ее вид. Найти ее основные характеристики (в зависимости от вида кривой):

- центр окружности, ее радиус;

- фокусы и эксцентриситет эллипса;

- фокусы и эксцентриситет гиперболы;

- вершину, фокус, ось и директрису параболы

№ варианта	Данные задачи
1	9х2 -16y2 - 144 = 0
2	7x2 + 16у2 - 112 = 0
3	12х2 + 5у2 - 60 = 0
4	3у = х2 + 4х - 11
5	х2 - 2х + 4у + у2 - 20 = 0;
6	5х2 - 10x + 3y2 + 6y + 7 = 0
7	4x2 + 25у2 - 100 = 0
8	3х2 - 4y2 = 12
9	х2 - 6х + 10у + у2 + 9 = 0.
10	х2 - 4у = 3